Essaie les exercices de DS, clique ci-dessous
Maths de première : exercice sur fonction trigonométrique sinus. Parité, périodicité, courbe, équations, intervalles, résolution graphique.
Exercice N°727 :
Exercice N°727 :
Soit f la fonction définie sur R par
f(x) = sin2 (x/2).
On note Cf la représentation graphique de f dans le plan graphique
(O ; →i ; →j).
1) Montrer que la fonction f est paire. Lis la suite »
Maths de première : exercice sur le cosinus et le sinus avec calculs. Trigonométrie, valeurs, équations, intervalles, mesure principale.
Exercice N°725 :
Exercice N°725 :
1-2-3) En utilisant les valeurs de cosinus et sinus à connaître et en traçant un schéma avec le cercle trigonométrique :
1) Déterminer la valeur exacte de sin(13π/6), Lis la suite »
Maths de première sur un algorithme et la trigonométrie, exercice corrigé, condition, si, alors, trigonométrique, boucle tant que.
Exercice N°603 :
Exercice N°603 :
Soit x l’une des mesures de l’angle orienté (→i ; →OM), où désigne un point du cercle trigonométrique.
Voici un algorithme qui doit permettre déterminer la mesure de x qui appartient à [0 ; 2π[.
1) Recopier et compléter la ligne 2. Lis la suite »
Exercice de maths de première : position relative de parabole et de droite. Inéquations équations, second degré, intersections, coordonnée.
Exercice N°259 :
Exercice N°259 :
1) Résoudre cette première inéquation sur R :
Maths de première sur les applications du produit scalaire : exercice avec Al-Kashi, triangles, angles, parallélogramme, formule.
Exercice N°675 :
Exercice N°675 :
ABCD est un parallélogramme tel que AB = 5, AD = 3 et D^AB = 60°.
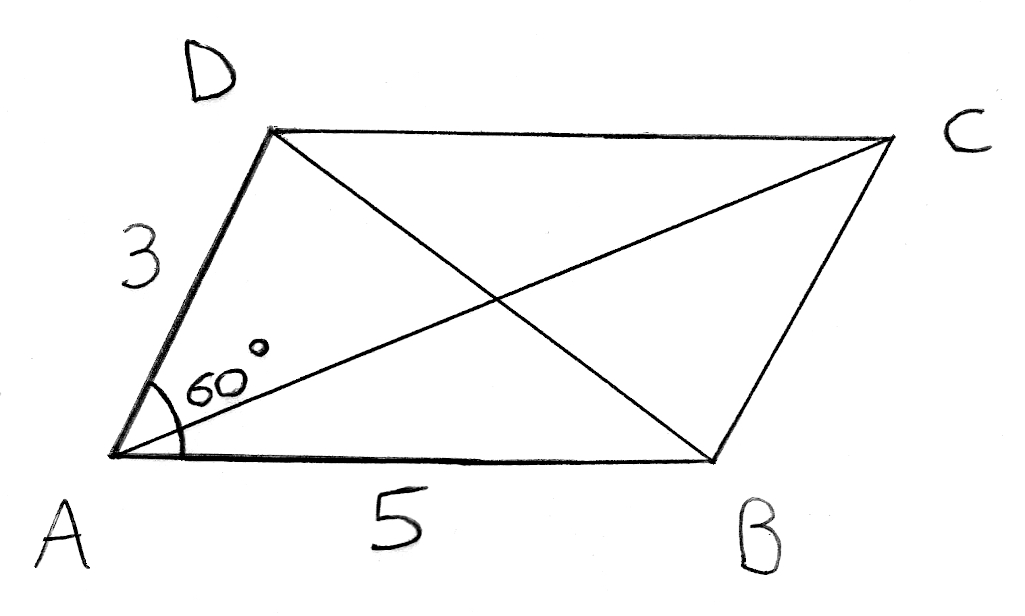
1) Calculer le produit scalaire →AB.→AD. Lis la suite »
Maths de première : exercice sur loi des sinus. Application du produit scalaire avec loi des sinus, théorème d’Al-Kashi, relation de Chasles.
Exercice N°672 :
Exercice N°672 :
Les bateaux d’Antonin (A) et de Brieuc (B) approchant de deux îles nommées C et D relèvent les mesures données sur le schéma ci-dessous.
On admet que le navire de Brieuc (B) est situé à 654,72 m de l’île D.
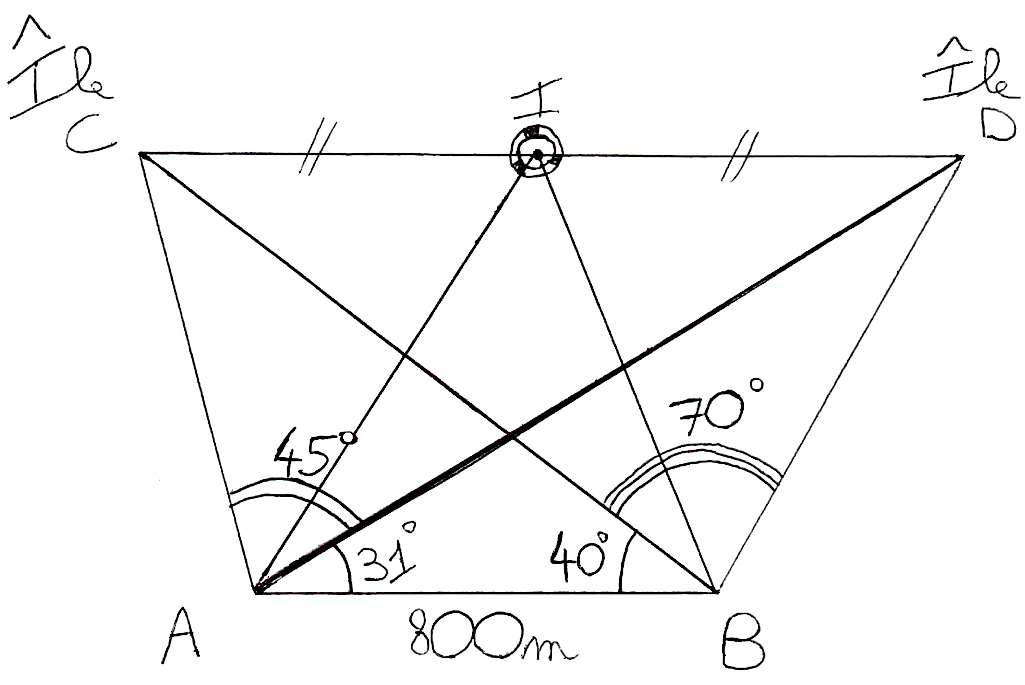
1) Déterminer la distance entre le navire de Brieuc et l’île C. Lis la suite »
Maths de seconde de statistique : exercice avec effectifs cumulés croissants, étendue, moyenne, fréquence, médiane, quartiles, mode.
Exercice N°001
Exercice N°001
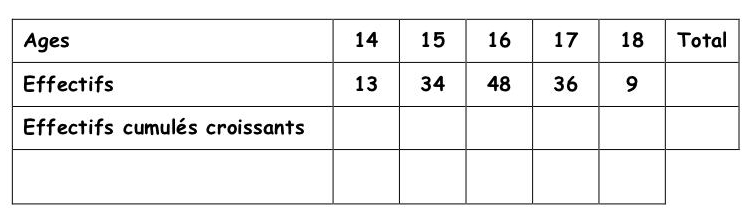
On donne, ci-dessus, la répartition par âge des élèves de seconde, âge révolu au premier janvier 2022.
1) Compléter la ligne effectifs cumulés croissants. Lis la suite »
Exercice de maths de première sur le produit scalaire avec triangle, rectangle, vecteurs, géométrie du plan, calcul, angle, cosinus.
Exercice N°022 :
Exercice N°022 :
ABCD est un rectangle, I est un point [DC] défini comme l’indique la figure ci-dessous.
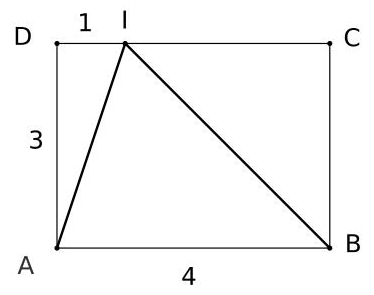
1) Démontrer que
(→ID + →DA).(→IC + →CB) = →ID.→IC+ DA2.
2) Calculer les longueurs AI et BI.
En déduire que : Lis la suite »
Exercice de maths de première sur l’algorithme et la somme des inverses avec boucles tant que et pour, variables, affectation.
Exercice N°616 :
Exercice N°616 :
On cherche à calculer la somme des inverses :
S = 1 + 1/2 + 1/3 + …… + 1/n
1) Calculer la valeur exacte puis la valeur approchée au millième de la somme des inverses pour n = 2, n = 3 et n = 4. Lis la suite »
Exercice sur dérivée et variation de première. Fonctions, intervalles de dérivabilité, calculs, tableaux, équation de la tangente.
Exercice N°045 :
Exercice N°045 :
La fonction f est définie et dérivable sur R par
f(x) = [(2x3)/3] + x2 – 13x + 4.
1) Calculer f ‘ (x). Lis la suite »
