Exercice de maths de première sur l’algorithme et la somme des inverses avec boucles tant que et pour, variables, affectation.
Exercice N°616 :

Exercice N°616 :
On cherche à calculer la somme des inverses :
S = 1 + 1/2 + 1/3 + …… + 1/n
1) Calculer la valeur exacte puis la valeur approchée au millième de la somme des inverses pour n = 2, n = 3 et n = 4.
On se donne le programme ci-dessous pour déterminer la valeur approchée au millième de la somme des inverses pour N donné.

2) Programmer ce premier algorithme en langage Python puis recopier et remplir le tableau suivant :
N | 5 | 20 | 100
S | … | …. | …..
On vaudrait maintenant connaître à partir de quel terme N la somme S dépasse la valeur 7. Pour cela, on écrit un deuxième algorithme, ci-dessous.
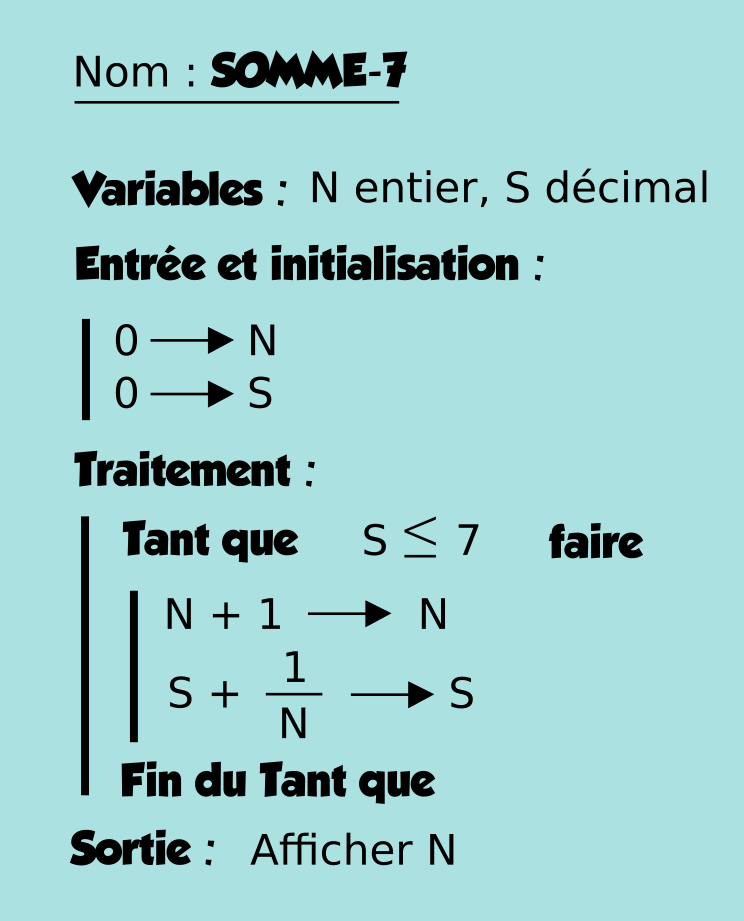
3) Expliquer la condition S ≤ 7 de la boucle conditionnelle “Tant que”.
4) Programmer ce second algorithme en langage Python
5) Donner la valeur de N affichée par le programme pour lequel la somme S dépasse la valeur 7.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : algorithme, somme des inverses.
Pour avoir le corrigé (57 centimes d’euros),
clique ici sur le bouton ci-dessous :
Pour avoir tous les corrigés actuels de ce chapitre (De 77 centimes à 1.97 euros selon le nombre d’exercices),
clique ici sur le bouton ci-dessous :
77 centimes pour 2 exercices – 97 cts pour 3 – 1.17€ pour 4 – 1.37€ pour 5 – 1.57€ pour 6 – 1.67€ pour 7 – 1.77€ pour 8 – 1.87€ pour 9 et 1.97€ pour 10 et +.
Exercice précédent : Droites – Sécantes ou parallèles, triangle et points d’intersection – Seconde

