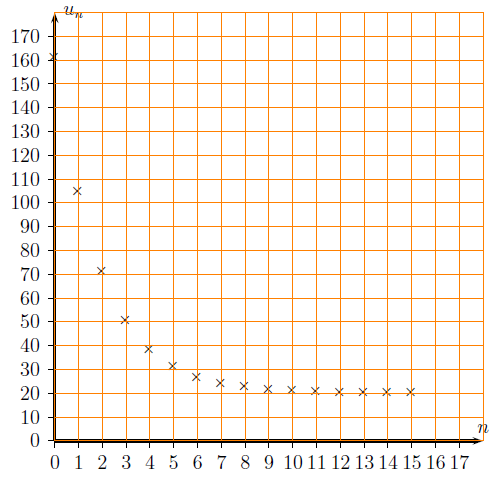
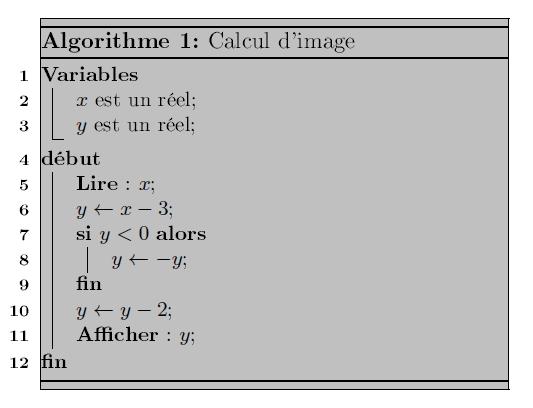
Exercice de maths de première sur l’algorithme et la somme des inverses avec boucles tant que et pour, variables, affectation.
Exercice N°616 :
Exercice N°616 :
On cherche à calculer la somme des inverses :
S = 1 + 1/2 + 1/3 + …… + 1/n
1) Calculer la valeur exacte puis la valeur approchée au millième de la somme des inverses pour n = 2, n = 3 et n = 4. Lis la suite »
Exercice de maths de première d’algorithme avec somme et suite géométrique. Formes récurrentes, forme explicite, boucle pour.
Exercice N°349 :
On considère la suite (un) définie pour tout entier naturel par :
{ u0 = 5,
{ un+1 = 2un – 3 si n ∈ N.
1) Calculer u1, u2 et u3. Lis la suite »
Exercice de maths avec algorithme, terminale, conjecturer, suite. Repère, graphique, auxiliaire géométrique, premier terme, raison, limite.
Exercice N°212 :
Exercice N°212 :
On donne ci-dessous la représentation graphique des 16 premiers termes d’une suite (un) dans le plan muni d’un repère orthogonal.
1) Conjecturer la limite de la suite (un). Lis la suite »
Exercice d’algorithmique de seconde avec boucle pour, variables, affectations, tableau, total, produit, initialisation, affichage.
Exercice N°591 :
Exercice N°591 :
On considère l’algorithme suivant :
1) Tester l’algorithme dans le tableau ci-dessous pour la valeur n = 5. Lis la suite »
Exercice de maths de seconde sur l’algorithmique avec exercice sur boucle tant que et boucle pour. Entrée, affectations et variables.
Exercice N°590 :
Exercice N°590 :
On considère l’algorithme suivant :
1) La valeur entrée de n est 3. Compléter le tableau suivant : Lis la suite »
Maths de seconde : exercice d’algorithme, condition, si, alors, sinon, fin si, variable, affectation, expression, entrée, sortie.
Exercice N°589 :
Exercice N°589 :
On considère un premier algorithme ci-dessous :
1) Si la valeur entrée de b est 10, la valeur affichée de a est a = ………. ? Lis la suite »
Exercice de maths de seconde avec algorithme, si, alors, sinon, entrée, sortie, conditions, variables, affectation, calculs, expressions.
Exercice N°588 :
Exercice N°588 :
On considère Le programme ci-dessous :
1) Déterminer la valeur de y affichée par l’algorithme lorsque l’utilisateur choisit x = 5. Lis la suite »
Maths de seconde : exercice d’algorithme avec antécédent, image, variable, condition, si, alors, sinon, fin si, fonction.
Exercice N°587 :
Exercice N°587 :
On donne l’algorithme ci-dessous :
1) Le faire fonctionner (à la main) avec les valeurs indiquées et compléter la deuxième colonne du tableau ci-dessous. Lis la suite »
Maths de seconde : exercice d’algorithme avec du repérage de seconde. Formules de géométrie, rédaction, variables, triangle isocèle.
Exercice N°585 :
Exercice N°585 :
Le plan est muni d’un repère orthonormé (O ; I ; J).
A(xA ; yA), B(xB ; yB) et C(xC ; yC) sont trois points du plan.
1) Compléter l’algorithme suivant, en rapport avec le chapitre Repérage, en expliquant ce qu’il fait. Lis la suite »
Maths de seconde : exercice, algorithme avec boucle pour, variable locale, coordonnées de points et segments à tracer, repère.
Exercice N°565 :
Exercice N°565 :
On donne l’algorithme suivant (réalisé avec Algobox) dans le lequel nous voyons une boucle “pour” :
1) L’appliquer, à la main, dans le repère ci-dessous en traçant bien tous les segments. Lis la suite »
