frenchmaths.com (par Sylvain Jeuland)

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) On a 4 chances sur 6 d’obtenir une rouge au premier tirage (et 2 chances sur 6 d’avoir une noire).
Si on a une rouge et qu’on la remet, on obtient les mêmes chances pour le second tirage.
Par contre, si on a une noire et qu’on ne la remet pas, on aura 4 chances sur 5 d’avoir une rouge et 1 chance sur 5 d’avoir une noire.

J’obtiens l’arbre suivant :

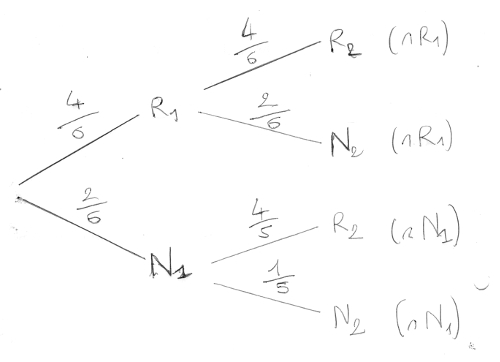
Les branches de droites forment la colonne des “sachants”.
Les probabilités tout à droite sont les “inter”.

P(boules rouges) = P(R₁ inter R₂)
= P(R₁) × P(R₂ sachant R₁)
= ⁴/₆ × ⁴/₆
= ²/₃ × ²/₃
= ⁴/₉

2) P(seconde boule noire) = P(N₂)
On retrouve N₂ deux fois sur la colonne de droite donc :

R₁ et N₁ forment une partition de Ω.
D’après la Formule des Probabilités Totales,
P(N₂) = P(R₁ inter N₂) + P(N₁ inter N₂)
= ⁴/₆ × ²/₆ + ²/₆ × ¹/₅
= ²/₃ × ¹/₃ + ¹/₃ × ¹/₅
= ²/₉ + ¹/₁₅
= ¹⁰/₄₅ + ³/₄₅
= ¹³/₄₅

3) P(première boule rouge sachant seconde noire) = P(R₁ sachant N₂)
= ^{P(R₁ inter N₂)}/_P(N2)
= ^(4/₆)/_(¹³/45)
= ⁴/₆ × ⁴⁵/₁₃
= ⁴/₂ × ¹⁵/₁₃ (en simplifiant par 3 en haut et en bas)
= ^2×15/₁₃
= ³⁰/₁₃

4) p est la probabilité de succès d’une épreuve.
Le succès est d’obtenir une boule rouge lors du tirage.
Il y a 4 boules rouges et n boules noires, soit (4+n) boules au total.
Comme les boules sont indiscernables au toucher, il y a équiprobabilité.
La probabilité d’obtenir une boule rouge (le succès) est donc le nombre de cas favorables divisé par le nombre total de cas.
Soit p = ⁴/_{(4 + n)}

5) On a du “au moins une”, on doit donc raisonner en contraire.
Le contraire de “l’une au moins des quatre boules tirées soit noire” est “toutes les boules sont rouges” donc :

q_n = P(l’une au moins des quatre boules tirées soit noire)
= 1 – P(X = 4)
= 1 – (Combinaison(n ; k) × p^k × (1 – p)^n-k)
= 1 – (Combinaison(4 ; 4) × p⁴ × (1 – p)^4-4)
= 1 – (1 × p⁴ × (1 – p)⁰)
= 1 – (p⁴ × 1)
= 1 – p⁴
= 1 – (⁴/_{(4 + n)})⁴

6) q_n ≥ 0,9999
⇔ 1 – (⁴/_{(4 + n)})⁴ ≥ 0,9999
⇔ – (⁴/_{(4 + n)})⁴ ≥ 0,9999 – 1
⇔ – (⁴/_{(4 + n)})⁴ ≥ -0,0001
⇔ (⁴/_{(4 + n)})⁴ ≤ 0,0001
⇔ (⁴/_{(4 + n)}) ≤ 0,0001^(1/4)
Comme tout est positif là, on enlève le puissance 4 à gauche, en faisant puissance 1/4 à droite.
⇔ ⁴/_{(4 + n)} ≤ 0,1
⇔ 4 ≤ 0,1 × (4 + n)
⇔ 4/0,1 ≤ 4 + n
⇔ 40 – 4 ≤ n
⇔ 36 ≤ n
⇔ n ≥ 36

36 est le plus petit entier naturel tel que q_n ≥ 0,9999

Bonne compréhension,
Sylvain Jeuland

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) Montrer que f de formule
f : x → ¹/_{(3x² + 4)}
est strictement croissante sur [−2 ; 0] et strictement décroissante sur [0 ; 2] :

Rédaction :

Je commence sur [−2 ; 0].

On prend -2 ≤ a < b ≤ 0 car on est sur [−2 ; 0]. Je prends en compte les bornes de l’intervalle qui vont me donner des informations.

-2 ≤ a < b ≤ 0

⇔ (-2)² ≥ a² > b² ≥ 0²

(on change le sens des inégalités

car la fonction “carré” est décroissante sur [−2 ; 0])

⇔ 3×4 ≥ 3×a² > 3×b² ≥ 3×0

(on garde le sens des inégalités quand on multiplie (ou divise) par un nombre positif, ici 3)

⇔ 12 + 4 ≥ 3×a² + 4 > 3×b² + 4 ≥ 0 + 4

(on garde le sens des inégalités car on ajoute (ou soustrait) un nombre)

⇔ ¹/₁₆ ≤ ¹/_{(3×a² + 4)} < ¹/_{(3×b² + 4)} ≤ ¹/₄

(on change le sens des inégalités car la fonction “inverse” est strictement décroissante sur [−2 ; 0])

⇔ ¹/₁₆ ≤ f(a) < f(b) ≤ ¹/₄

a < b donne f(a) < f(b) donc f est strictement croissante sur [−2 ; 0].

De même, sur [0 ; 2] :

On prend -2 ≤ a < b ≤ 0 car on est sur [0 ; 2]. Je prends en compte les bornes de l’intervalle qui vont me donner des informations.

-2 ≤ a < b ≤ 0

⇔ 0² ≥ a² < b² ≥ 2²

(on garde le sens des inégalités car la fonction “carré” est croissante sur [0 ; 2])

⇔ 3×0 ≤ 3×a² < 3×b² ≤ 3×4

(on garde le sens des inégalités quand on multiplie (ou divise) par un nombre positif, ici 3)

⇔ 0 + 4 ≤ 3×a² + 4 < 3×b² + 4 ≤ 12 + 4

(on garde le sens des inégalités car on ajoute (ou soustrait) un nombre)

⇔ ¹/₄ ≥ ¹/_{(3×a² + 4)} > ¹/_{(3×b² + 4)} ≥ ¹/₁₆

(on change le sens des inégalités car la fonction “inverse” est strictement décroissante sur [0 ; 2])

⇔ ¹/₄ ≥ f(a) > f(b) ≥ ¹/₁₆

a < b donne f(a) > f(b) donc f est strictement décroissante sur [0 ; 2].

Pour résumer, voici le tableau de variation de la fonction f :

2) Tableau de variations de g sur [−2 ; 2] avec
g(x) = − √f(x) + ¹/₂ :

Rédaction :

On peut rédiger de la même manière avec
a < b donne f(a) < f(b) ou f(a) > f(b)
mais je vais choisir la méthode des tableaux de variation.

Je reprends le tableau de variation de f et je lui applique la fonction “racine” car f(x) subit l’effet de la racine en premier lieu.

Les valeurs des fractions sont mises à la racine. Les 1 restent 1, 16 devient 4 et 4 devient 2.

Les variations ne changent pas car la fonction “racine” est strictement croissante sur R⁺.

On note que les contenus de la racine sont positifs : ¹/₄ et ¹/₁₆.

En second lieu, le nombre √f(x) est multiplié par (-1) en témoigne le “moins” devant lui. Comme on multiplie par un nombre négatif, les variations changent et les images sont aussi multipliées par (-1). Cela donne le tableau :

Enfin pour obtenir la fonction g, on ajoute ¹/₂ à l’ensemble. Comme on ajoute un nombre, les variations ne changent pas. Seules les valeurs se voient augmentées de ¹/₂ ci-dessous :

3) Encadrement de g(x) sur [−2 ; 2] :

On voit d’après la tableau de signe que
0 ≤ g(x) ≤ ¹/₄.
Il a été utile de calculer toutes les images des bornes des intervalles.

Bonne compréhension,
Sylvain Jeuland

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) f : x → -3x² sur ]-∞ ; 0] :

Rédaction de la méthode 1 :

On prend a < b ≤ 0 car on est sur ]-∞ ; 0].

a < b ≤ 0

⇔ a² > b² ≥ 0²
(on change le sens des inégalités car la fonction “carré” est strictement décroissante sur ]-∞ ; 0])

⇔ -3a² < -3b² ≤ -3×0
(on change le sens des inégalités car on multiplie par un nombre négatif)

⇔ f(a) < f(b) ≤ 0

a < b donne f(a) < f(b) donc f est strictement croissante sur ]-∞ ; 0].

Rédaction de la méthode 2 :

2) g : x → 2√(x) – 3 sur [0 ; +∞[ :

Rédaction de la méthode 1 :

On prend 0 ≤ a < b car on est sur [0 ; +∞[.

0 ≤ a < b

⇔ √(0) < √(a) ≤ √(b)
(on garde le sens des inégalités car la fonction “racine” est strictement croissante sur [0 ; +∞[)

⇔ 2√(0) < 2√(a) ≤ 2√(b)
(on garde le sens des inégalités car on multiplie par un nombre positif, ici 2)

⇔ 0 – 3 < 2√(a) – 3 ≤ 2√(b) – 3
(on garde le sens des inégalités quand on ajoute ou on soustrait)

-3 < f(a) ≤ f(b)

a < b donne f(a) < f(b) donc f est strictement croissante sur [0 ; +∞[.

Rédaction de la méthode 2 :

3) h : x → ¹/_|x| sur R^* :

Rédaction de la méthode 2 uniquement :

La fonction que l’on a là est l’inverse de la fonction absolue. Donc je représente les variations de la fonction “valeur absolue” ci-dessous.
D’après le cours, on obtient la première ligne :

Comme la fonction “inverse” est strictement décroissante sur R^– et sur R⁺. On change le sens des variations de la valeur absolue pour obtenir celles de h ci-dessus.

4) l : x → -1 + ( ¹/_{(2x + 4)} ) sur ]-2 ; +∞[ :

Rédaction de la méthode 1 :

On prend 0 ≤ a < b car on est sur [-2 ; +∞[.

-2 ≤ a < b

⇔ 2×(-2) < 2a ≤ 2b
(on garde le sens des inégalités car on multiplie par un nombre positif, ici 2)

⇔ -4 + 4 < 2a + 4 ≤ 2b + 4
(on garde le sens des inégalités quand on ajoute ou on soustrait)

⇔ 0 < 2a + 4 ≤ 2b + 4

(ici on a zéro à gauche, la partie gauche va disparaître quand on va passer à l’inverse)

⇔ ¹/_{(2a + 4)} ≥ ¹/_{(2b + 4)}

(on change le sens des inégalités car la fonction “inverse” est strictement décroissante sur ]0 ; +∞[. Ici on s’aperçoit que nos valeurs sont strictement au-dessus de zéro)

⇔ -1 + ¹/_{(2a + 4)} ≥ -1 + ¹/_{(2b + 4)}
(on garde le sens des inégalités quand on ajoute ou on soustrait)

⇔ f(a) ≥ f(b)

a < b donne f(a) > f(b) donc f est strictement décroissante sur [-2 ; +∞[.

Rédaction de la méthode 2 :

Bonne compréhension,
Sylvain Jeuland

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) f(x) = x + 1 + xe^-x
= x + 1 + u(x) × v(x)
avec u(x) = x
donc u'(x) = 1
avec v(x) = e^-x
donc v'(x) = -e^-x

f'(x) = 1 + 0 + u'(x) × v(x) + u(x) × v'(x)
= 1 + 1 × e^-x + x × (-e^-x)
= 1 + e^-x – xe^-x

f'(x) = 1 + e^-x – u(x) × v(x)
avec les mêmes u(x) et v(x).

Donc f ”(x) = 0 – e^-x – (u'(x) × v(x) + u(x) × v'(x))
= – e^-x – (1 × e^-x – xe^-x)
= -2e^-x + xe^-x
= (x – 2)e^-x.

2) x-2 est négatif avant 2, puis positif après 2.
Un exponentiel est toujours strictement positif.

car f'(0) = 1 + e^-0 – 0e^-0
= 1 + 1 + 0
= 2

et f'(2) = 1 + e^-2 – 2e^-2
= 1 – e^-2.

3) D’après le tableau de variation, on voit que le minimum de la fonction est
1 – e^-2 qui est strictement positif.
Donc f'(x) > 0 sur les réels positifs.

4) f(x) = x + 1 + xe^-x

lim_{[x → +∞]} (x + 1) = +∞

Comme xe^-x est positif sur R⁺, peu importe sa limite (0, une constante ou +∞), additionnée à la limite +∞ de (x + 1), on aura :

lim_{[x → +∞]} f(x) = +∞

5) On sait que f'(x) est toujours positif sur R⁺, donc f est strictement croissante.
f(0) = 0 + 1 + 0e^-0
= 1.

6) L’équation d’une tangente est :

Donc ici y = f'(1)(x – 1) + f(1).

f'(1) = 1 + e^-1 – 1e^-1
= 1.

f(1) = 1 + 1 + 1e^-1
= 2 + e^-1.

Donc y = 1(x – 1) + 2 + e^-1
y = x + 1 + e^-1.

7) * f est continue sur R⁺
* f est strictement croissante sur R⁺

f(0) = 1
lim_{[x → +∞]} f(x) = +∞

* Donc 2 appartient à l’intervalle image [ 1 ; +∞ ]
soit [ f(0) ; lim_{[x → +∞]} f(x)].

D’après le théorème des valeurs intermédiaire, l’équation f(x) = 2 admet une unique solution α sur R⁺.

On trouve α à l’aide de la calculatrice avec la tableur.
Tout d’abord, on part de 0 et on monte de 1 en 1 jusqu’à dépasser 2.
Donc 0 < α < 1 car on dépasse 2 dès l’abscisse x = 1.

Maintenant on va de 0.1 en 0.1 :

On dépasse 2 à partir de 0.7 donc 0.6 < α < 0.7

Maintenant on va de 0.01 en 0.01 :

On dépasse 2 à partir de 0.66 donc 0.65 < α < 0.66

Maintenant on va de 0.001 en 0.001 :

On dépasse 2 à partir de 0.659 donc 0.658 < α < 0.659

Je prends 0.659 comme valeur arrondie de α.

8)

Cf est la courbe bleue et (T) la droite rouge qui est bien la tangente en 1.

Bonne compréhension,
Sylvain Jeuland

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) Dérivation de f(x) = 2x³ − 3x + 2 :

Rédaction :

f(x) est un polynôme donc on dérive chaque monôme terme à terme.
f ‘(x) = 2 × 3x² – 3 + 0
= 6x² – 3.

2) Dérivation de g(x) = −²/_x³ :

Rédaction :

On divise par x³, ce qui n’est pas facile.
Quand on a un x^positif dans un dénominateur, l’idéal est d’avoir un x^négatif au numérateur.
On utilise donc la formule suivante.

Du coup, ¹/_x³ = x^-3.

Et −²/_x³
= -2 × ¹/_x³
= -2 × x^-3

Pour dériver ce g(x), on garde le -2 qui est un coefficient multiplicatif et on dérive le x^-3 à l’aide de la formule ci-dessous.

Donc g'(x) = -2 × (-3) × x^-3-1
= 6 × x^-4
= ⁶/_x⁴
en repassant la puissance négative au dénominateur (en exposant positif).

3) Dérivation de h(x) = ¹/_{(3x² + 1)} :

Rédaction :

h(x) est de la forme ¹/_(v(x))
avec v(x) = 3x² + 1,
donc v'(x) = 3 × 2x + 0 = 6x.

On utilise la formule suivante :

Donc h'(x) = –^(v'(x))/_(v(x))²
= –^(6x)/_{(3x² + 1)²}.

4) Dérivation de i(x) = ^{(x − 1)}/_{(x + 1)} :

Rédaction :

i(x) est de la forme ^(u(x))/_(v(x))
avec u(x) = x − 1,
donc u'(x) = 1,
avec v(x) = x + 1,
donc v'(x) = 1.

On utilise la formule suivante de la dérivée d’un quotient :

Donc i'(x) = ^{(u'(x) × v(x) – u(x) × v'(x))}/_(v(x))²
= ^{(1 × (x + 1) – 1 × (x – 1))}/_{(x + 1)²}
= ^{((x + 1) – (x – 1))}/_{(x + 1)²}
= ^{(x + 1 – x + 1)}/_{(x + 1)²}
= ²/_{(x + 1)²}.

5) Dérivation de j(x) = ^{(x2 + 2x)}/₃ − ²/_x :

Déjà, la première fraction, c’est un divisé par 3. Ce n’est pas un “vrai” quotient avec x en bas.

Rédaction :

j(x) = ¹/₃ × (x² + 2x) − 2 × ¹/_x

La dérivée du polynôme “x² + 2x” est classique.
Pour dériver ¹/_x, on utilise la formule suivante :

Donc j'(x) = ¹/₃ × (2x + 2) – 2 × (-¹/_x²)
= (²/₃)x + ²/₃ + ²/_x²

6) Dérivation de k(x) = 3(x² + 1)² :

Rédaction :

k(x) est de la forme 3 × (u(x))²
avec u(x) = x² + 1,
donc u'(x) = 2x.

La dérivée d’une fonction mise à la puissance n est :

Donc k'(x) = 3 × 2 × u'(x) × (u(x))^2-1
= 6 × 2x × (x² + 1)¹
= 12x × (x² + 1)
= 12x³ + 12x.

Exercice : Clic droit vers le corrigé

Tout le corrigé :

1) Montrer que C, I et J sont alignés :

Rédaction :

C, I et J sont alignés, si et seulement si, les vecteurs ^→CI et ^→IJ sont colinéaires. J’ai donc besoin des coordonnées de ces vecteurs, donc je dois calculer les coordonnées de C, I et J avant.

Cette figure est composé de trois carrés dont celui de gauche ABGH. Comme ^→AB et ^→AH ne sont pas colinéaires (côtés du carré), on peut introduire le repère (A ; ^→AB ; ^→AH).

Cela veut dire que le point A a pour coordonnées (0 ; 0), B(1 ; 0) et H(0 ; 1).
Du coup, on a C(2 ; 0), D(3 ; 0), E(3 ; 1), F(2 ; 1) et G(1 ; 1).

Calculons les coordonnées du point I :

I est le milieu de [AG].
Les coordonnées d’un milieu pour deux points A et B sont :

Du coup, je calcule ceci pour [AG].

x_I = ^{(x_A + x_G)}/₂
= ^{(0 + 1)}/₂
= ¹/₂

y_I = ^{(y_A + y_G)}/₂
= ^{(0 + 1)}/₂
= ¹/₂

Du coup, les coordonnées de I sont (¹/₂ ; ¹/₂).

Calculons les coordonnées du point J :

L’abscisse de J est 1 car J est sur [BG] et [BG] relie deux points d’abscisses 1.
L’ordonnée de J est la distance qui le sépare de B, c’est à dire BJ, car l’ordonnée de B est de 0 et car (BJ) est parallèle à la droite (AH) avec ^→AH le vecteur “ordonnées” du repère.

Pour calculer (BJ), on utilise le théorème de Thalès dans le triangle ADE avec :
* (DE) // (BJ),
* (BD) et (JE) sécantes en A,
* A,B,D puis A,J,E alignés dans le même sens.

Du coup, le rapport BJ/DE est égale à AB/AD qui est de ¹/₃ car [AD] c’est trois fois le côté [AB]. Comme DE = 1, on a BJ = ¹/₃, qui donne l’oordonnée du point J ¹/₃.

Du coup, J(1 ; ¹/₂).

Calcul des coordonnées des vecteurs ^→CI et ^→IJ :

x_^→CI
= x_I – x_C
= ¹/₂ – 2
= –³/₂

y_^→CI
= y_I – y_C
= ¹/₂ – 0
= ¹/₂

x_^→IJ
= x_J – x_I
= 1 – ¹/₂
= ¹/₂

y_^→IJ
= y_J – y_I
= ¹/₃ – ¹/₂
= ²/₆ – ³/₆
= –¹/₆

Les deux vecteurs sont colinéaires si et seulement si leurs coordonnées x et x’, puis y et y’ sont proportionnelles.

On a donc le tableau :
–³/₂ | ¹/₂
¹/₂ | –¹/₆

Les produits en croix sont :
–³/₂ × –¹/₆
= +³/₁₂
= ¹/₄
Et :
¹/₂ × ¹/₂
= ¹/₄

Donc les produits en croix sont égaux, x’y – xy’ = 0, les coordonnées sont proportionnelles, donc les vecteurs ^→CI et ^→IJ sont colinéaires et les points C, I et J sont alignés.

2) Montrer que Dm est une droite :

Rédaction :

Quelque soit le m, l’équation mx + (2m – 1)y + 4 = 0
est de la forme ax + by + c = 0 qui est l’équation cartésienne d’une droite.

Du coup, les Dm sont des droites.

3) Trouver m tels que Dm parallèle aux axes :

Rédaction :

D_m est parallèle à l’axe des abscisses si l’équation
est de la forme y = constante.
Ce qui équivaut à y – constante = 0 en mode “équation cartésienne”.
Pour cela, il faut que le coefficient devant x, le “a” soit égal à zéro.
Ce coefficient est “m”. Du coup D_{1 est parallèle à l’axe des abscisses pour m = 0.}

D₁ est parallèle à l’axe des ordonnées si l’équation
est de la forme x = constante.
Ce qui équivaut à x – constante = 0 en mode “équation cartésienne”.

Pour cela, il faut que le coefficient devant y, le “b” soit égal à zéro.
Ce coefficient est (2m – 1). Du coup D_m est parallèle à l’axe des abscisses pour 2m – 1 = 0 soit m = ¹/₂.

4) Équation des droites D₀ et D₁ et point d’intersection :

Rédaction :

L’équation est mx + (2m – 1)y + 4 = 0.

D₀ : 0x + (2 × 0 – 1)y + 4 = 0
⇔ – 1y + 4 = 0
⇔ y = 4.

D₁ : 1x + (2 × 1 – 1)y + 4 = 0
⇔ x + 1y + 4 = 0.

Le point d’intersection, que j’appelle I, est à la fois sur D₀ et D₁ donc les coordonnées de I respectent à la fois les deux équations, donc le système suivant :

{ y = 4
{ x + y + 4 = 0
(Les deux petites accolades sont en fait une seule grande accolade)

⇔
{ y = 4
{ x + 4 + 4 = 0

⇔
{ y = 4
{ x + 8 = 0

⇔
{ y = 4
{ x = -8

Les coordonnées du point d’intersection I sont (4 ; -8).

5) Montrer que que Dm passe par un point fixe :

Rédaction :

Si toutes les droites Dm passent par un point fixe, c’est le point fixe qu’on vient de trouver juste au dessus. C’est à dire I(4 ; -8).

Je dois donc prouver que ce point I appartient à toutes les droites Dm. Donc que ses coordonnées vérifient l’équation-égalité Dm quel que soit le m.

Du coup, quel que soit m,
Gauche = mx + (2m – 1)y + 4
= m × (-8) + (2m – 1) × 4 + 4
= -8m + 8m – 4 + 4
= 0m + 0
= 0 = Droite.

Donc l’équation des droites Dm est vérifiée par ce point. Donc toutes les droites appartiennent à un point fixe quel que soit m.

Bonne compréhension,
Sylvain Jeuland

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) Rédaction :

Pour montrer qu’une fonction est impaire, il faut montrer que l’image de -x par la fonction g vaut l’opposé de l’image de x. Soit g(-x) = -g(x).

Donc pour tout x,
g(-x) = tan(-x) – (-x)
= -tan(x) + x (car la fonction tan est impaire : sin/cos donc impaire/paire qui est impaire car -/+ donne -)
= -(tan(x) – x)
= -g(x).
Donc g est impaire.

2) Rédaction :

En –^Π/₂ supérieur :

lim_{[x → –^Π/2 sup]} tan(x) = -∞.
lim_{[x → –^Π/2 sup]} x = –^Π/₂ sup.

Par somme/différence, lim_{[x → –^Π/2 sup]} g(x) = -∞.

De la même manière, lim_{[x → +^Π/2 inf]} g(x) = +∞ (car tan tend vers +∞).

3) Rédaction :

Pour étudier les variations de g, calculons sa dérivée.
Pour tout x,
g(x) = tan(x) – x
donc pour tout x,
g'(x) = tan'(x) – 1

Donc g'(x) = (tan(x))² + 1 – 1 = (tan(x))².

Comme un carré est toujours positif ou nul, (tan(x))² est toujours positif. Il sera nul seulement en 0 car seul tan(0) = 0.

Le tableau est donc :

4) Rédaction :

g(0) = tan(0) – 0 = 0 – 0 = 0.
Je mets la valeur 0 dans le tableau ci-dessus.

5) Rédaction :

Pour tout x,
f(x) = tan(x) – x – ^x3/₃

pour tout x,
f'(x) = tan'(x) – 1 – 3^x2₃

Donc f'(x) = (tan(x))² + 1 – 1 – ^{x2
= (tan(x))2 – x2.}

6) Rédaction :

f'(x) = (tan(x))² – x²
= a² – b² (troisième identité remarquable)
= (a – b)(a + b)
= [tan(x) – x] × [tan(x) + x]
= g(x) × [tan(x) + x]

x et tan(x) sont négatifs avant 0 et positifs après 0, donc leur somme également.
Le tableau de signe est :

7) Rédaction :

Comme f'(x) est positif sur Df, f est croissante sur Df.

8) Signe de f(x) et inégalité :

Rédaction

On a la variation de f et,
f(0) = tan 0 – 0 – 0 = 0 – 0 – 0 = 0.
Donc le tableau est :

On a donc f(x) ≤ 0 sur ] –^Π/₂ ; 0 ]
et f(x) ≥ 0 sur [ 0 ; ^Π/₂ [.

Donc tan x – x – ^x3/₃ ≤ 0 sur ] –^Π/₂ ; 0 ].
Et tan x – x – ^x3/₃ ≥ 0 sur [ 0 ; ^Π/₂ [.

Du coup, tan x ≤ x + ^x3/₃ sur ] –^Π/₂ ; 0 ].
Et tan x ≥ x + ^x3/₃ sur [ 0 ; ^Π/₂ [.

Donc ce n’est pas vrai pour les x positifs.

Bonne compréhension,
Sylvain Jeuland

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) Rédaction :

Pour avoir les variations de f, faisons la dérivée f'(x).

f(x) = ^(u(x))/_(v(x))
avec u(x) = x² + 2,
donc u'(x) = 2x + 0 = 2x,
v(x) = 1 − 2x,
donc v'(x) = 0 – 2 = -2.

Du coup, f'(x) = ^{(u'(x)×v(x) – u(x)×v'(x))}/_(v(x))²
= ^{(2x×(1 − 2x) – (x2 + 2)×(-2))}/_{(1 − 2x)²}
= ^{(2x − 4x2 – [-2x2 – 4])}/_{(1 − 2x)²}
= ^{(2x − 4x2 + 2x2 + 4)}/_{(1 − 2x)²}
= ^{(−2x2 + 2x + 4)}/_{(1 − 2x)²}.

Pour étudier le signe de f'(x), on fait un tableau de signe avec chaque facteur et diviseur. L’un est −2x² + 2x + 4 et le diviseur est (1 − 2x)²

Un carré est toujours positif ou nul. Donc (1 − 2x)² est toujours strictement positif ou nul quand 1-2x vaut 0. Cela arrive quand x=¹/₂. En cette valeur, le carré est nul, mais comme il est au dénominateur, cela fera une double-barre dans le tableau de f'(x) car la fraction n’est pas définie pour x=¹/₂.

Pour le signe de −2x² + 2x + 4, qui est du second degré, on fait :
Δ = b² – 4ac
= 2² – 4 × (-2) × 4
= 4 + 32 = 36 > 0.

Donc deux racines :
x₁ = ^{(-b – √Δ)}/_(2a)
= ^{(-2 – √36)}/_{(2 × (-2))}
= ^{(-2 – 6)}/_(-4)
= ^-8/_-4
= 2

x₂ = ^{(-b + √Δ)}/_(2a)
= ^{(-2 + √36)}/_{(2 × (-2))}
= ^{(-2 + 6)}/_(-4)
= ⁴/_12-4
= -1

a = -2 donc le trinôme est négatif à l’extérieur des racines -1 et 2. Du coup, on obtient le tableau suivant :

J’ai aussi déterminé le signe de f(x) à l’aide des variations et des valeurs.

2) Rédaction :

L’équation d’une tangente est :

Donc en a = 0,
y = f'(0) (x – 0) + f(0).

f'(0) = ^{(−2×02 + 2×0 + 4)}/_{(1 − 2×0)²}
= ⁴/_1²
= 4

f(0) = ^{(02 + 2)}/_{(1 – 2×0)}
= ²/₁
= 2

Donc l’équation de la tangente à Cf au point d’abscisse 0 est
y = 4(x – 0) + 2 = 4x + 2.

3) Rédaction :

g est déjà continue sur chacun des intervalles séparément (f est rationnelle définie avant 0 et 3x + m est affine). Il faut donc juste faire en sorte que g soit continue en 0.

Pour que g soit continue en 0, il faut que la limite de g(x) en 0 “-moins” et 0 “+plus” soit la même, et qu’elles soient égales à g(0).
Quand l’un des deux côtés est défini, ici c’est le cas pour 0 à gauche car la borne 0 de l’intervalle ]-∞ ; 0] est fermée, la limite est juste l’image.
Donc limite de g(x) quand x tend vers 0 “-moins” = g(0) = f(0) = 2 (expression de la première ligne).

Pour la limite à droite en 0 “+plus”, il faut donc trouver m tel qu’elle soit égale à 2 (qui est l’image g(0)) pour que la fonction g soit continue en 0.

lim _{[x → 0+]} 3x = 0
lim _{[x → 0+]} m = m
Par somme, lim _{[x → 0+]} (3x + m) = m
Donc lim _{[x → 0+]} g(x) = m
Pour que c’est limite à droite soit égale 2, m doit être égal à 2.

Donc m = 2.

4) Rédaction :

Déjà g est dérivable sur ]-∞ ; 0] car elle vaut f qui est dérivable avec comme dérivée en 0, f'(0) = 2.
Sur ] 0 ; +∞ [, g est affine donc la dérivée est le coefficient directeur 3.
La limite en zéro à droite de la dérivée est donc 3.
Or à gauche g'(0) = 2, à droite la limite de g’ en 0+ est 3. Les valeurs sont différentes donc g n’est pas dérivable en 0.

Bonne compréhension,
Sylvain Jeuland

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) Rédaction :

Le sommet d’une parabole est donné par les coordonnées α et β du cours de maths. Je préfère les appeler x_S et y_S. Les formules sont :

Ici a = -3, b = 6, c = 12.

x_S = ^-b/_2a = ^-6/_(2(-3))
= ^-6/_-6 = 1

Δ = b² – 4ac
= 6² – 4 × (-3) × 12
= 36 + 4 × 3 × 12
= 36 + 144
= 180

y_{S = ^-Δ/4a = ^-180/(4(-3))
= ^-12/-6 = 15}

On peut calculer aussi l’ordonnée du sommet y_S en prenant l’image f(x_S). On peut aussi utiliser α et β pour nommer l’abscisse et l’ordonnée du sommet.

Donc les coordonnées du sommet S sont (1 ; 15).

2) Rédaction :

Comme on a les coordonnées du sommet, on sait où s’arrêtent les flèches.
Regardons le signe de “a”. C’est -3 donc il est négatif.

(Hors-rédaction : l’atmosphère/ambiance est négative, la parabole ne sourit pas.)

Du coup, la parabole monte puis descend. De même pour les flèches. J’obtiens le tableau de variation suivant.

Pour dessiner une courbe, il faut faire un tableau de valeurs. Par exemple de 1 en 1 en partant de (-3).

(Tu peux le faire à la calculatrice à l’aide de la fonction table. Ou alors tu dessines le tableau sur la copie en calculant un par un en mettant bien des parenthèses autour des nombres négatifs. Quand c’est espacé en hauteur, tu peux calculer de demi en demi : 0.5, 1.5, etc)

3) Rédaction :

3x² – 4x – 4 > -3x² + 6x + 12
⇔ 3x² – 4x – 4 – (-3x² + 6x + 12) > 0
⇔ 3x² – 4x – 4 + 3x² – 6x – 12 > 0
⇔ 6x² – 10x – 16 > 0

Pour résoudre une inéquation plus grand ou plus petit que 0, je dois faire un tableau de signe.

Comme c’est du second degré, je calcule le discrimant
Δ = b² – 4ac
= (-10)² – 4 × 6 × (-16)
= 100 + 384 = 484 > 0

Donc on a deux racines x₁ et x₂ :

x₁ = ^{(-b – √Δ)}/_(2a)
= ^{(-(-10) – √484)}/_{(2 × 6)}
= ^{(10 – 22)}/₍₁₂₎
= ^-12/₁₂
= -1

x₂ = ^{(-b + √Δ)}/_(2a)
= ^{(-(-10) + √484)}/_{(2 × 6)}
= ^{(10 + 22)}/₍₁₂₎
= ³²/₁₂
= ⁸/₃

Le tableau de signe est de la forme (on rappelle que a > 0) :

Donc on prend seulement les “plus+” et pas les zéros car l’inégalité est stricte.

S = ]-∞ ; -1[ U ]⁸/₃ ; +∞[

4) Rédaction :

3x² – 4x – 4 > -3x² + 6x + 12
C’est quand f(x) > g(x) d’après les données.
C’est quand la courbe C_f est strictement au dessus de la courbe C_g.

Si on entoure les portions de courbe qui conviennent et qu’on redescend verticalement sur l’axe des abscisses, on retrouve la réunion d’intervalle précédente.

5) Rédaction :

A_g est égale à la moitié de l’aire du carré ABCD
⇔ A_g = 0.5 × A_ABCD
⇔ AM² + (AB-AM)² = 0.5 × AB²

On pose x = AM (ça marche toujours comme ça dans ce style d’exercice).

⇔ x² + (8 – x)² = 0.5 × 8²
⇔ x² – 8² + 2 × 8 × x + x² = 0.5 × 64
⇔ x² + 64 – 16x + x² = 32
⇔ 2x² – 16x + 64 – 32 = 0
⇔ 2x² – 16x + 32 = 0

Comme tous les coefficients sont paire, je simplifie cette équation par 2 pour simplifier.

⇔ x² – 8x + 16 = 0

Je peux résoudre avec le discriminant Δ mais je préfère ici utiliser une identité remarquable.

⇔ x² – 2 × 4 × x + 16 = 0
⇔ (x – 4)² = 0
⇔ x – 4 = 0 (Un carré est nul si et seulement si son contenu est nul).
⇔ x = 4

Donc AM = 4 et il existe une seule position de M qui convient à cette égalité d’aires. C’est le milieu de [AB].

Bonne compréhension,
Sylvain Jeuland

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) Sur l’écran de votre calculatrice, tracer (P) et (D) et conjecturer le nombre de points d’intersection de (P) et (D).

Rédaction :

Ce n’est pas très précis. Je conjecture qu’il y a un point d’intersection entre (P) et (D).

2) Déterminer par le calcul les abscisses des points d’intersection de (P) et (D).

Rédaction :

Je donne des noms aux deux fonctions associées à (P) et (D).

p(x) = -9x² + 60x – 80
d(x) = 5x + 4

Pour trouver les points d’intersection des deux courbes, il faut qu’elles sont la même hauteur (image) pour le le même “x”.
Je résous :

(P) et (D) se coupent quand
p(x) = d(x)
⇔ -9x² + 60x – 80 = 5x + 4
⇔ -9x² + 60x – 80 – (5x + 4) = 0
⇔ -9x² + 60x – 80 – 5x – 4 = 0
⇔ -9x² + 55x – 84 = 0

Δ = b² – 4ac
= 55² – 4 × (-9) × (-84)
= 3025 – 3024
= 1 > 0

Donc il y a deux solutions distinctes.

x₁ = ^{(-b – √Δ)}/_(2a)
= ^{(-55 – √1)}/_{(2 × (-9))}
= ^(-56)/_((-18))
= ²⁸/₉

x₂ = ^{(-b + √Δ)}/_(2a)
= ^{(-55 + √1)}/_{(2 × (-9))}
= ^(-54)/_((-18))
= 3

Du coup, (P) et (D) ony deux points d’intersection, en x = 3 et x = ²⁸/₉.

3) Déterminer la forme canonique de f :

Rédaction :

On a f(x) = 2x² + 2x – 24.
La forme canonique d’une fonction du second degré est :

x^S = α = abscisse du sommet
y^S = β = ordonnée du sommet

Ces coordonnées (x^S ; y^S) sont données par :

Ici a = 2, b = 2, c = -24.

x_S = ^-b/_2a = ^-2/_(2×2)
= ^-2/₄
= ^-1/₂

Δ = b² – 4ac
= 2² – 4 × 2 × (-24)
= 4 + 4 × 2 × 24
= 4 + 192
= 196

y_{S = ^-Δ/4a = ^-196/(4×2)
= ^-196/8
= ^-49/2}

Donc les coordonnées du sommet S sont (2 ; –⁴⁹/₂).

On peut aussi calculer y_S avec
f(x_S) = f(^-1/₂) = 2 × ^(-1/₂₎² + 2 × ^(-1/₂₎ – 24
= 2 × ¹/₄ – 1 – 24
= ¹/₂ – ²/₂ – ⁴⁸/₂
= –⁴⁹/₂

4) Factoriser f(x) :

Rédaction :

Comme Δ est positif, il y a deux racines x1 et x2 (quand c’est nul, x1 = x2).
La forme factorisée d’un polynôme du second degré est :

Ici a = 2, b = 2, c = -24, Δ = 196

x₁ = ^{(-b – √Δ)}/_(2a)
= ^{(-2 – √196)}/_{(2 × 2)}
= ^{(-2 – 14)}/₍₄₎
= ^-16/₄
= -4

x₂ = ^{(-b + √Δ)}/_(2a)
= ^{(-2 + √196)}/_{(2 × 2)}
= ^{(-2 + 14)}/₍₄₎
= ¹²/₄
= 3

Donc la forme factorisée est f(x) = 2 × (x – (-4)) × (x – 3).

5) Coordonnées des points d’intersection de (C) avec l’axe des abscisses et avec l’axe des ordonnées :

Rédaction :

Les points d’intersections de (C) avec l’axe des abscisses, c’est quand f(x) = 0.
J’ai déjà résolu cette équation en 4).
C’est pour x = -4 et x = 3. Et leur ordonnée y vaut 0.
Donc ces points sont (0 ; -4) et (0 ; 3).

Si (C) coupe l’axe des ordonnées (ce qui donnera ce point d’intersection), c’est que l’abscisse x est égal à 0 car l’axe des ordonnées a pour équation x = 0.
Pour le calcul de l’ordonnée, je rassemble y = f(x) et x = 0, cela fait y = f(0).
y = f(0) = 2 × 0² +2 × 0 – 24
= -24.
Le point d’intersection a pour coordonnées (0 ; -24).

6) Position de (C) par rapport à l’axe des abscisses :

(C) est au dessus de l’axe des abscisse quand f(x) > 0 et est en dessous quand f(x) < 0.

Comme a = 2 > 0 (ambiance/atmosphère positive : la parabole sourit), la parabole est tournée vers le haut.
Comme Δ > 0, la parabole coupe deux fois l’axe des abscisses.
De plus, la trinôme est du signe de a à l’extérieur des racines.

Voici le tableau de position relative :

Bonne compréhension,
Sylvain Jeuland