Maths : exercice sur dérivée et exponentielle de terminale. Équations, inéquations, dérivées, limites, tableau de variations, asymptotes.
Exercice N°275 :
Exercice N°275 :
1-6) Résoudre les équations suivantes :
1) ex = -4, Lis la suite »
Exponentielle – Equation, dérivée, limite, variation – Terminale
12 octobre 2022
Maths : exercice d’exponentielle avec variation de première. Fonction, équation, produit nul, inéquation, inégalité, dérivée.
Exercice N°662 :
Exercice N°662 :
1) Étudier les variations de la fonction f définie sur R par :
f(x) = (-2x + 3)ex. Lis la suite »
Maths de première : exercice d’exponentielle avec équations et variation. Fonction, inéquations, calculs de dérivées, tableau de signe.
Exercice N°660 :
Exercice N°660 :
1-6) Résoudre les équations suivantes :
1) ex = -4 Lis la suite »
Exponentielle – Inéquations, équations, dérivées – Première
26 novembre 2021
Exercice de maths sur équation et inéquation, exponentielle de première. comparaisons de puissances, calculs de dérivées, formules.
Exercice N°336 :
Exercice N°336 :
1-6) Résoudre dans R :
1) e−2x−1 > 0, Lis la suite »
Exponentielle – Équation, continuité, suite, récurrence – Terminale
13 novembre 2021
Exercice de maths sur la fonction exponentielle, suite, récurrence, terminale, continuité, équations, convergence, raisonnement, variations.
Exercice N°284 :
Exercice N°284 :
Le but de l’exercice est de démontrer que l’équation (E) ∶
xex = 1
admet une unique solution dans l’ensemble R des nombres réels, et de construire une suite qui converge vers cette unique solution.
Existence et unicité de la solution :
On note f la fonction définie sur R par
f(x) = x − e−x.
1) Démontrer que x est solution de l’équation (E)
si et seulement si f(x) = 0. Lis la suite »
Exercice de maths de terminale sur le bac 2016 sur la fonction, intégrale, primitive, logarithme népérien, dérivée, variation, TVI, surface.
Exercice N°600 :
Exercice N°600 :
La courbe (C) ci-dessous représente, dans un repère orthonormé, une fonction f définie et dérivable sur [0.5 ; 6]. Les points A(1 ; 3) et B d’abscisse 1,5 sont sur la courbe (C).
Les tangentes à la courbe (C) aux points A et B sont aussi représentées en pointillés sur ce graphique, la tangente au point B est horizontale.
On note f ‘ la fonction dérivée de f.
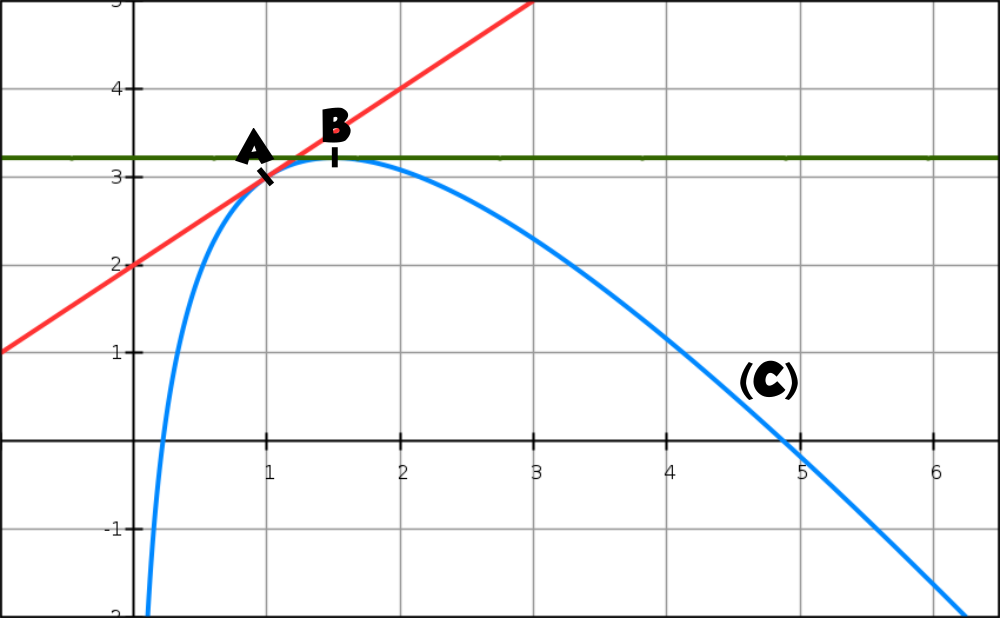
Les parties A et B sont indépendantes.
Partie A : Étude graphique
1) Déterminer f ‘ (1,5). Lis la suite »
Exponentielle – Tangente, première, dérivées, variation – Première
5 septembre 2021
Maths : exercice d’exponentielle avec tangente de première. Dérivées, tableau de variation, inconnues, système d’équations, graphique.
Exercice N°751 :
Dans le plan muni d’un repère orthogonal, la courbe C ci-dessous représente une fonction f définie sur R.
La tangente D à la courbe C au point A(0 ; -4) passe par le point
B(2 ; -6).
1) Donner la valeur de f(0). Lis la suite »
Exponentielle – Continuité, équation, tableau, variation – Terminale
5 septembre 2021
Maths de terminale : exercice d’exponentielle avec continuité et équation. Tableau de variation, solution unique, encadrement.
Exercice N°750 :
Exercice N°750 :
On considère la fonction f définie sur R par
f(x) = (-4x2 + 5)e-x + 3.
On note (C) la courbe représentative de la fonction f dans un repère orthogonal.
On note f ‘ la dérivée de f sur R.
1) Démontrer que pour tout réel x ∈ R,
f ‘ (x) = (4x2 – 8x – 5)e-x. Lis la suite »
Exponentielle – Continuité, équation, solution unique – Terminale
5 septembre 2021
Maths de terminale : exercice d’exponentielle avec variation et continuité, équation avec solution unique, coût de production, primitive.
Exercice N°749 :
Exercice N°749 :
Soit f la fonction définie sur [0 ; 5] par
f(x) = (ax + b)e−x
où a et b sont deux réels.
On note f ‘ la fonction dérivée de f.
1) Montrer que pour tout nombre réel x,
f ‘ (x) = (a − b − ax)e−x. Lis la suite »
Exponentielle – Bénéfice, dérivée, variation, maximum – Première
5 septembre 2021
Maths : exercice d’exponentielle avec bénéfice de première. Dérivée, variation, maximum, quantité, production, inéquation, nombre dérivé..
Exercice N°748 :
La courbe (C) donnée ci-dessous est la représentation graphique dans un repère orthogonal d’une fonction f définie et dérivable sur [2 ; 9]. On note f ‘ sa fonction dérivée.
Les points A(3 ; e) et B(4 ; 2) appartiennent à cette courbe.
La tangente à la courbe en A est parallèle à l’axe des abscisses et la tangente (T) à la courbe en B coupe l’axe des abscisses au point d’abscisse 6.
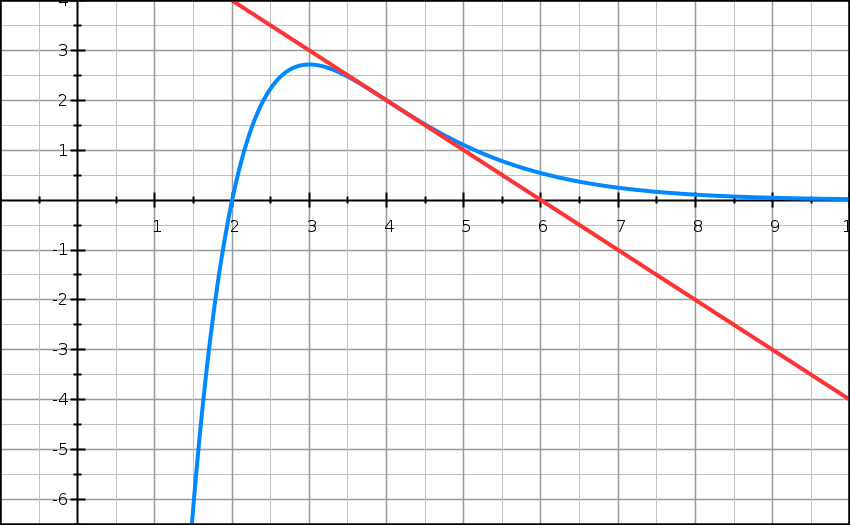
1-2) Par lecture graphique, répondre aux deux questions suivantes, sans justifier.
1) Pour quelles valeurs du nombre réel x de l’intervalle [3 ; 9] a-t-on
f(x) ≤ 2 ? Lis la suite »
