Exercice de maths de première : position relative de parabole et de droite. Inéquations équations, second degré, intersections, coordonnée.
Exercice N°259 :
Exercice N°259 :
1) Résoudre cette première inéquation sur R :
Exercice sur dérivée et variation de première. Fonctions, intervalles de dérivabilité, calculs, tableaux, équation de la tangente.
Exercice N°045 :
Exercice N°045 :
La fonction f est définie et dérivable sur R par
f(x) = [(2x3)/3] + x2 – 13x + 4.
1) Calculer f ‘ (x). Lis la suite »
Dérivation – Calculs, racine, rationnelle, courbe – Première
27 octobre 2022
Maths de première : exercice sur la dérivabilité avec pente de tangente. Calculs, formules, racines, fonctions rationnelles, courbe.
Exercice N°296 :
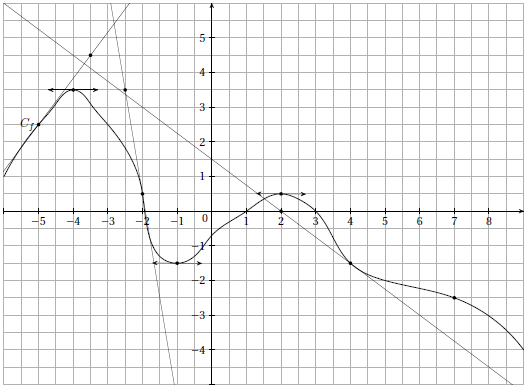
Voici ci-dessus la courbe représentative Cf d’une fonction f définie sur R.
1) D’après le graphique, donner la valeur de f ‘ (−4) en justifiant. Lis la suite »
Maths de première : exercice sur la dérivation, fonction, bénéfice, coût moyen, tableau de variations, maximal, minimal, étude de signe.
Exercice N°294 :
Exercice N°294 :
Une entreprise produit des appareils électroménagers.
Le coût horaire de production de x appareils est donné en euros par :
C(x) = x2 + 50x + 100
pour 5 ≤ x ≤ 100.
L’entreprise vend chaque appareil 100 euros.
1) Justifier que le bénéfice horaire réalisé par la fabrication et la vente de x appareils est :
B(x) = −x2 + 50x − 100
pour x ∈ [5 ; 100]. Lis la suite »
Dérivation – Polynôme, coût, bénéfice, variations – Première
27 octobre 2022
Maths de première sur la dérivation : exercice de dérivée de polynôme avec coût, recette, bénéfice, calculs, recette,variation, maximum.
Exercice N°290 :
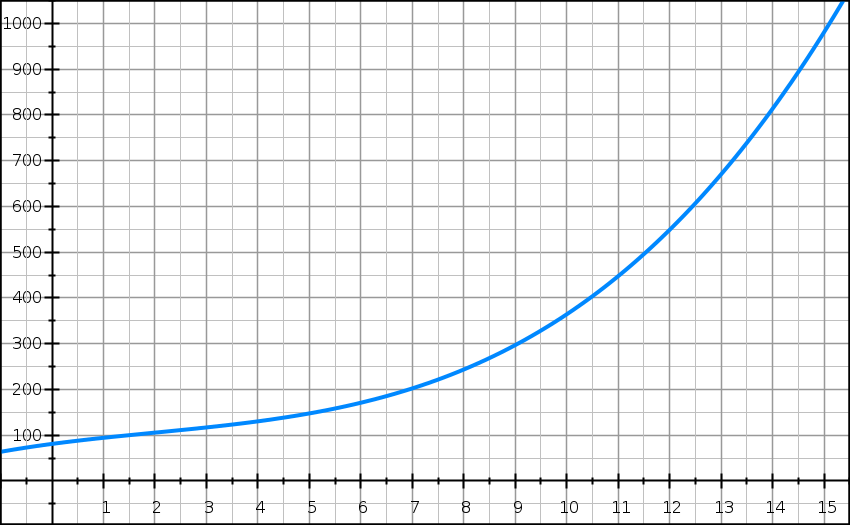
Soit C la fonction définie pour tout réel x élément de l’intervalle ]0 ; 15] par :
C(x) = x3/3 − 2x² + 15x + 81.
La fonction C modélise le coût total de production, exprimé en milliers d’euros, de x milliers d’articles fabriqués. La courbe CT représentative de la fonction C est tracée ci-dessus dans un repère orthogonal.
On suppose que chaque article produit est vendu au prix de 60 €.
On note R(x) la recette, exprimée en milliers d’euros, générée par la production et la vente de x milliers d’articles.
1) Dans le repère précédent, tracer la courbe représentative de la fonction recette. Lis la suite »
Suites – Variation, forme explicite, fonction, tableau, sens – Première
12 septembre 2022
Maths : exercice de suites et variation en première. Forme explicite, fonction, tableau de variation, étude de signe, sens.
Exercice N°815 :
Exercice N°815 :
1) Étudier le sens de variation de la suite (an) définie pour tout entier naturel par la forme explicite :
an = -3n + 1. Lis la suite »
Maths : exercice sur le Nombre d’Or de première. Second degré, parabole, trajectoire, sommet, tableau de variation, forme canonique.
Exercice N°799 :
Exercice N°799 :
On considère les deux réels Φ = (1 + √5)/2 et Ψ = (1 – √5)/2.
Le nombre Φ est appelé le nombre d’or. Soit f la fonction polynôme du second degré définie sur R par l’expression :
f(x) = x2 – x – 1.
1) Montrer que Φ et Ψ sont les antécédent de 0 par f. Lis la suite »
Exercice de maths sur la fonction de référence cube de seconde. Tracer courbe, équations, inéquations, résolutions graphiques, solutions.
Exercice N°734 :
Exercice N°734 :
1) Représenter dans le repère orthogonal ci-dessous (unité 1 cm en abscisse, 2 mm en ordonnée) la fonction
f : x → x3
sur l’intervalle [2.5 ; 3]. Lis la suite »
Maths de première : exercice de dérivation avec fonction rationnelle. Tableau de variation, définition du nombre dérivé, calcul, coefficient.
Exercice N°292 :
Exercice N°292 :
Soit f une fonction définie et dérivable sur l’intervalle ]−1/2 ; +∞[ dont le tableau des variations est donné ci-dessous.
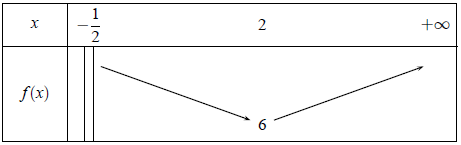
1) On note f ‘ la dérivée de la fonction f. Déterminer f ‘ (2). Lis la suite »
Maths de première : exercice d’exponentielle avec équations et variation. Fonction, inéquations, calculs de dérivées, tableau de signe.
Exercice N°660 :
Exercice N°660 :
1-6) Résoudre les équations suivantes :
1) ex = -4 Lis la suite »
