Limites et croissance comparée exponentielle. Exercice de maths de terminale avec calculs, produits, quotients et morceaux de polynômes.
Exercice N°827 :
Exercice N°827 :
1-8) Déterminer dans chaque cas la limite des fonctions contenant la fonction exponentielle ci-dessous et préciser l’asymptote si celle-ci existe bien.
1) lim x → -∞ ( 4xex + 3ex – 2 ). Lis la suite »
Maths de terminale avec limites : exercice d’exponentielle avec croissance comparée, fraction, factorisation, plus ou moins l’infini.
Exercice N°826 :
Exercice N°826 :
1-8) Déterminer dans chaque cas la limite des fonctions contenant la fonction exponentielle ci-dessous et préciser l’asymptote si celle-ci existe bien.
1) f(x) = x – ex, en +∞. Lis la suite »
Maths de première : exercice de limites de suites avec algorithme, encadrements, seuils, calculs de termes, conjecture, programmation Python.
Exercice N°825 :
Exercice N°825 :
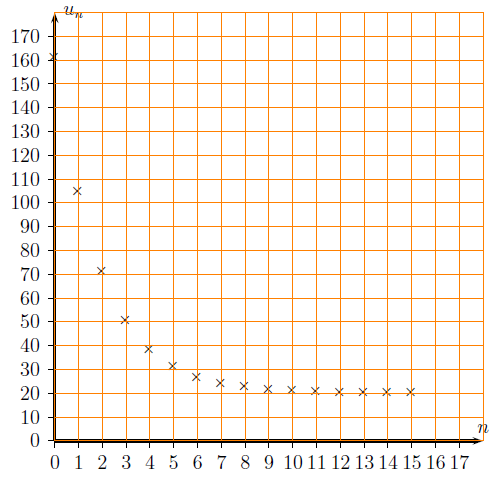
1-2-3-4) Des glaciologues étudient les variations du niveau de la mer depuis la fin de la dernière ère glaciaire (environ –13000 ans). n milliers d’années après cette date, ils notent un la variation, en mètres, du niveau de la mer et posent :
vn = 280/(2 + 68 × 0,6n).
1) Calculer v0, v10 et v20 et donner une valeur approchée au dixième. Lis la suite »
Maths de première : exercice de limites de suites explicites. Formules, géométrique, arithmétique, conjectures, seuils, calculs, algorithme.
Exercice N°824 :
Exercice N°824 :
1-2-3-4) Soit (un) le suite définie sur N par :
un = -n2 + 2n + 3.
1) Calculer u0, u5 et u10. Lis la suite »
Maths de première : exercice sur les limites et les suites géométriques avec conjectures, algorithme, interprétation, calculs de termes.
Exercice N°823 :
Exercice N°823 :
Soit (un) une suite définie sur N par :
un = 3n.
1) Après quelques calculs, conjecturer la limite de (un). Lis la suite »
Exercice de maths sur les limites de suites et conjectures en première. Forme explicite, inégalités et rangs, somme géométrique de termes.
Exercice N°822 :
Exercice N°822 :
Soit (un) une suite définie sur N par :
un = 2 – 1/(n2 + 1).
1) Après quelques calculs, conjecturer la limite de (un). Lis la suite »
Exercice de maths sur les limites de suites de première avec rang, inégalités, forme explicite, puissance, fraction, valeur absolue.
Exercice N°821 :
Exercice N°821 :
Première partie :
Soit (un) une suite définie sur N par :
un = 106/(n + 1).
1) Donner les valeurs des premiers termes u0, u1, u2, puis de u10, u100, u(104) et u(106). Lis la suite »
Maths : exercice de limites de suites de première avec calculs de termes, conjectures, formes explicites et récurrentes, variation.
Exercice N°820 :
Exercice N°820 :
Soit (un) une suite définie sur N par :
u0 = 5
et pour tout entier naturel
un+1 = 2un – 6.
1) Après quelques calculs, conjecturer la limite de (un). Lis la suite »
Maths : exercice sur dérivée et exponentielle de terminale. Équations, inéquations, dérivées, limites, tableau de variations, asymptotes.
Exercice N°275 :
Exercice N°275 :
1-6) Résoudre les équations suivantes :
1) ex = -4, Lis la suite »
Exercice de maths avec algorithme, terminale, conjecturer, suite. Repère, graphique, auxiliaire géométrique, premier terme, raison, limite.
Exercice N°212 :
Exercice N°212 :
On donne ci-dessous la représentation graphique des 16 premiers termes d’une suite (un) dans le plan muni d’un repère orthogonal.
1) Conjecturer la limite de la suite (un). Lis la suite »
