Maths : exercice sur fonction convexe de terminale. Courbe, équation de tangente, point d’inflexion, nombre dérivé, variation, signe.
Exercice N°307 :
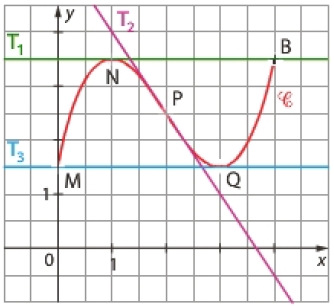
f est une fonction définie et deux fois dérivable sur [0 ; 4] dont on donne la représentation graphique C ci-dessous.
Les tangentes T1 et T3 sont parallèles à l’axe des abscisses respectivement aux points N et Q.
T2 est la tangente à C au point P(2 ; 5/2) et le point P est un point d’inflexion de la courbe C.
1) Déterminer f ‘ (1), f ‘ (2) et f ‘ (3) graphiquement en justifiant la réponse donnée.
2) Déterminer une équation de la tangente T2.
3) Déterminer f ‘ ‘ (2) en justifiant la réponse donnée.
4) Rappeler la définition d’une fonction convexe sur un intervalle I de R et déterminer la convexité de f.
5) En déduire les variations de f ‘ et le signe de f ‘ ‘ (x).
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, fonction convexe, terminale.
Exercice précédent : Convexité – Fonctions, courbes, dérivée, inflexion – Terminale

