Exercice : Clic droit vers l’exercice
Tout le corrigé :
1) Exprimer Y = cos(x + 2π) – sin(π – x) + cos(π + x) – sin(-x) :
Tu vois quatre termes différents qu’il faut gérer en quatre étapes.
D’abord cos(x + 2π) :
Ajouter 2π à l’angle x, c’est faire un tour complet de cercle trigo et revenir à l’angle x.
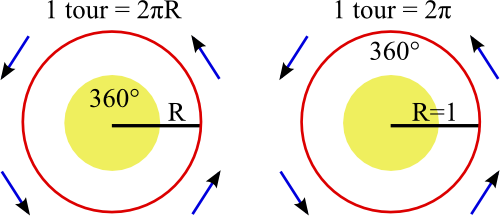
Cela veut dire que le fait d’ajouter 2π, d’enlever 2&pPi;, ou des multiples de 2π (4π, 6π, etc) ne change à la valeur du cosinus (et du sinus).
On a donc comme formule : Pour tout x, cos(x + 2π) = cos(x).
Ensuite sin(π – x)
Dans les questions comme ça avec des π-x, des π+x, etc, il faut toujours se ramener un quart de cercle Nord-Est pour dessiner x. Ce quart Nord-Est représente le cos(x) et le sin(x).
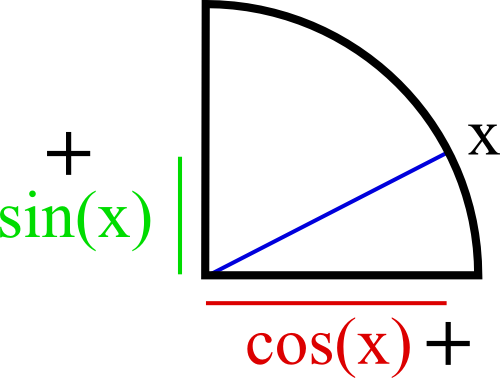
J’attire ton attention sur une chose, tu vois cet angle x plus bas que haut, en dessous de π/4.
Il y a un trait horizontal qui fait la largeur en dessous de l’angle, c’est le cosinus en rouge.
Il y a un trait vertical qui fait la hauteur à gauche de l’angle, c’est le sinus en vert.
Les deux traits ont différentes longueurs ici.
Et comme l’angle est en haut à gauche, le sinus et le cosinus sont tous les deux positifs (indiqués par le signe +).
Maintenant, il faut dessiner π-x pour comparer ! C’est là que tu dois dessiner le cercle trigo avec x en haut à droite et le π-x.
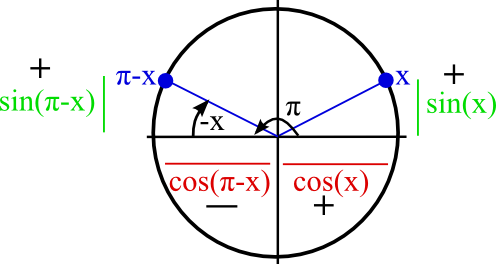
En haut à droite, tu retrouves l’angle x avec son cosinus rouge en largeur et son sinus vert ne hauteur.
Comme l’angle est à droite, le cosinus est positif (+).
Comme l’angle est au dessus de l’axe des abscisse, le sinus est positif (+).
Pour trouver l’emplacement π-x, tu vas tout à gauche puis tu remontes à l’envers pour enlever le x (du même écartement/angle) que le x à droite.
Là encore, il faut tracer le trait horizontal en dessous de l’angle. C’est la largeur cosinus(π-x) rouge.
Comme ce cosinus va vers la gauche de l’axe des ordonnées, il est négatif.
Là encore, tu peux tracer le trait vertical à côté de l’angle. C’est la hauteur sinus(π-x) vert. Comme ce sinus va au dessus de l’axe des abscisses, il est positif.
Il faut comparer les longueurs des traits cos(π-x) et sin(π-x) avec ceux de cos(x) et sin(x). Ces longueurs sont les valeurs !
On s’aperçoit que les traits des cosinus ont même longueur donc:
cos(π-x) = +cos(x) ou cos(π-x) = -cos(x).
On regarde les signes, l’un des cosinus est “moins-“ et l’autre est “plus+”.
Du coup, cos(π-x) = -cos(x) car ils n’ont pas le même signe.
De plus, on s’aperçoit que les traits des sinus ont même longueur donc:
sin(π-x) = +sin(x) ou sin(π-x) = -sin(x).
On regarde les signes, les deux sinus sont “plus+”.
Du coup, sin(π-x) = +sin(x) car ils sont de même signe.
Conclusion et Rédaction : D’après le cours, sin(π – x) = sin(x).
Puis cos(π + x)
Même méthode. On refait un cercle trigonométrique analogue au précédent. Cette fois, tu vas jusqu’à π à gauche et tu continues pour ajouter +x. Le sinus sera cette fois vers le bas car on repasse en dessous de l’axe des abscisses : il est donc négatif.

Il faut comparer les longueurs des traits cos(π+x) et sin(π+x) avec ceux de cos(x) et sin(x). Ces longueurs sont les valeurs !
On s’aperçoit que les traits des cosinus ont même longueur donc:
cos(π+x) = +cos(x) ou cos(π+x) = -cos(x).
On regarde les signes, l’un des cosinus est “moins-“ et l’autre est “plus+”.
Du coup, cos(π+x) = -cos(x) car ils n’ont pas le même signe.
On s’aperçoit que les traits des sinus ont même longueur donc:
sin(π+x) = +sin(x) ou sin(π+x) = -sin(x).
On regarde les signes, l’un des sinus est “moins-“ et l’autre est “plus+”.
Du coup, sin(π+x) = -sin(x) car ils n’ont pas le même signe.
Conclusion et Rédaction : D’après le cours, cos(π + x) = -cos(x).
Enfin sin(-x)
Dessine le cercle, c’est surtout la droite du cercle qui servira.
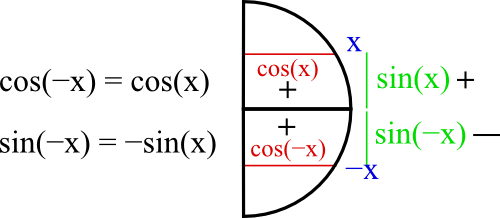
Compare les cosinus de -x et x. Ils sont identiques car ils vont tous les deux vers la droite.
Compare les sinus de -x et x. Ils sont opposés car l’un va vers le haut et l’autre vers le bas.
Conclusion et Rédaction : D’après le cours, sin(-x) = -sin(x).
Rassemblons tout :
Rédaction :
Y = cos(x + 2π) – sin(π – x) + cos(π + x) – sin(-x)
= cos(x) – sin(x) + (-cos(x)) – (-sin(x)) (d’après ce qu’on a vu plus haut)
= cos(x) – sin(x) – cos(x) + sin(x)
= 0.
Donc Y = 0.
2) Exprimer Z = 2sin(x + 5π) + cos(x + π/2) + cos(x) – 3sin(x + π/2) :
Tout d’abord sin(x + 5π) :
Comme vu plus haut, il y a trop de π dans 5π. Comme la fonction sinus est périodique de période 2π, on peut enlever des 2π sans problème.
Rédaction :
sin(x + 5π)
= sin(x + 3π) (car sin est 2π-périodique)
= sin(x + 1π) (car sin est 2π-périodique)
= sin(π + x)
= -sin(x) (d’après le cours et vu dans la question 1)).
Ensuite cos(x + π/2) :
Celui-là n’est pas facile, c’est reparti pour le dessin d’un cercle trigonométrique avec l’angle x en haut à droite. Comme on ajoute π/2), tu dessineras l’angle x+π/2 un quart de tour plus loin (car π/2 c’est un quart de tour et π c’est un demi-tour).
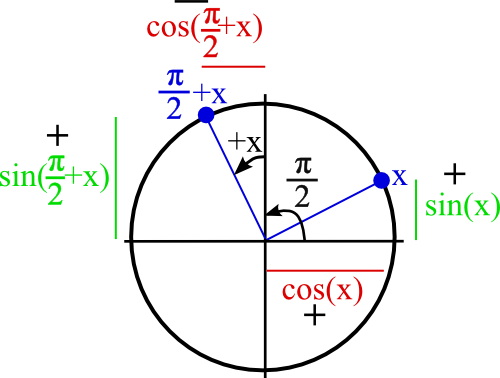
Comparons maintenant le cos(x + π/2) avec cos(x) et sin(x).
Si tu regardes de près les longueurs, celle de cos(x + π/2) en rouge est égale à celle de sin(x) en vert (les petites longueurs).
Or, cos(x + π/2 est vers la gauche, il est dans les “moins-“. Et sin(x) est vers le haut, il est dans les “plus+”.
Donc ils ne sont pas de même signe. Du coup :
cos(x + π/2) = -sin(x)
Comparons maintenant le sin(x + π/2) avec cos(x) et sin(x).
Si tu regardes de près les longueurs, celle de sin(x + π/2) en vert est égale à celle de cos(x) en rouge (les grandes longueurs).
Or, sin(x + π/2 est vers le haut, il est dans les “plus+”. Et cos(x) est vers la gauche, il est dans les “plus+”.
Donc ils sont de même signe. Du coup :
sin(x + π/2) = cos(x)
Conclusion et Rédaction : D’après le cours, cos(x + π/2) = -sin(x).
Enfin sin(x + π/2) :
C’est la situation précédente.
Rédaction : D’après le cours, sin(x + π/2) = cos(x).
Rassemblons tout :
Z = 2sin(x + 5π) + cos(x + π/2) + cos(x) – 3sin(x + π/2)
= 2(-sin(x)) + (-sin(x)) + cos(x) – 3cos(x) (d’après ce qu’on a vu précédemment)
= -3sin(x) – 2cos(x).
Donc Z = -3sin(x) – 2cos(x).
3) Démontrer que : (→AB, →AD) + (→DA, →DC) + (→CD, →CB) + (→BC, →BA) = 0 :
Déjà, tu peux voir qu’il y a des vecteurs opposés. Ce serait bien de retrouver les mêmes vecteurs partout. Par exemple transformons →DA = –→AD.
Rédaction :
En partant du membre de gauche :
(→AB, →AD) + (→DA, →DC) + (→CD, →CB) + (→BC, →BA)
= (→AB, →AD) + (-→AD, –→CD) + (→CD, –→BC) + (→BC, –→AB) (***)
Que faire avec les moins ?
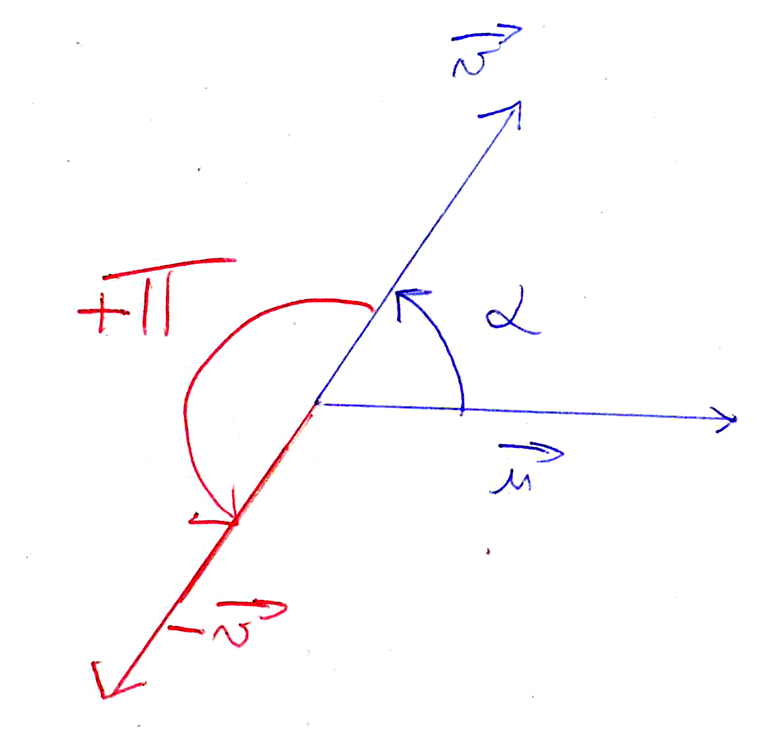
Enlever un “moins-” à un vecteur, c’est prendre son opposé. La conséquence sur les angles est qu’on ajoute π car on fait un demi-tour supplémentaire en prenant l’opposé.
On voit sur le dessin que :
(→u, –→v) = (→u, ->v) + π.
Ajoutons π à chaque fois qu’on enlève un “moins-” à un vecteur.
Rédaction :
(***)
= (→AB, →AD) + (→AD, →CD) + π + π + (→CD, →BC) + π + (→BC, →AB) + π
= (→AB, →AD) + (→AD, →CD) + (→CD, →BC) + (→BC, →AB) + 4π
= (→AB, →AD) + (→AD, →CD) + (→CD, →BC) + (→BC, →AB) + 0 (car les multiples de 2π font des angles nuls)
= (→AB, →CD) + (→CD, →BC) + (→BC, →AB) (avec la relation de Charles, on peut enlever les deux vecteurs →AD qui se suivent car si tu vas de →u vers →v, puis de →v vers →w, c’est comme aller de →u vers →w)
= (→AB, →BC) + (→BC, →AB) (idem avec →CD)
= (→AB, →AB) (idem avec →AB)
= 0 (car il n’y a pas d’angle entre deux fois le même vecteur).
Bonne compréhension,
Sylvain Jeuland

