frenchmaths.com (par Sylvain Jeuland)

Exercice : Clic droit vers le corrigé

Tout le corrigé :

1) Pour tracer les droites d’équations y = x
et y = 0.85x + 1.8, on choisit deux valeurs de x (ici 0 et 10) puis on calcule leurs images y. Cela donne deux points de coordonnées x et y que l’on place. On trace l’unique droite qui passe par ces deux points.

2) Partons du u₀ et déterminons les autres termes par ricochet sur les deux droites. La droite y = 0.85x + 1.8 représente la suite u_n+1 = 0.85u_n + 1.8.

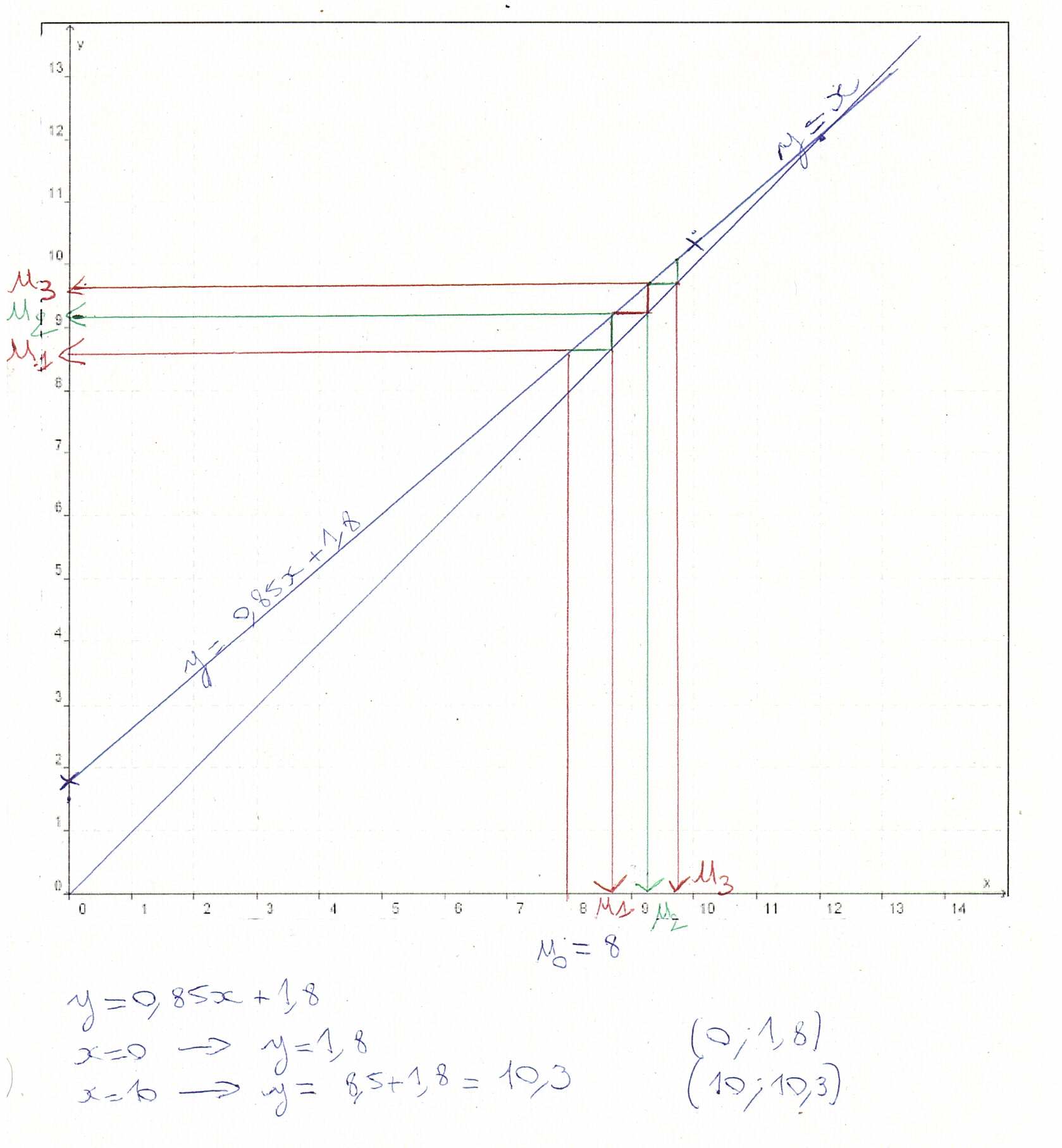
3) Comme l’intersection des deux droites se fait pour x = 12, et que les segments des u_n semblent aller vers cette intersection, je conjecture que la limite de la suite est 12.

4) On a pour tout n entier naturel, v_nn – 12.
On sait aussi que u_n+1 = 0,85×u_n + 1.8.

Pour prouver qu’une suite (v_n) est géométrique, il faut arriver à :
Pour tout n entier naturel, v_n+1 = q*v_n, donc on écrit sur la feuille :

Pour tout n entier naturel,
v_n+1 = u_n+1 – 12 (on fait appel à l’égalité entre v_n et u_n)
= 0,85×u_n + 1.8 – 12 (on fait appel à l’égalité entre u_n+1 et u_n)
= 0,85×u_n – 10,2
= 0,85×( u_n – 10,2/0,85 ) (on factorise par le coefficient devant u_n)
= 0,85×( u_n – 10,2/0,85 )
= 0,85×( u_n – 12 )
= 0,85×v_n (on refait appel à l’égalité entre u_n+1 et u_n dans l’autre sens)

Il existe un réel q réel (q = 0,85), tel que pour tout n entier naturel,
v_n+1 = q×v_n,
donc (v_n) est une suite géométrique de raison 0,85 et de premier terme v₀
= u₀ – 12
= 8 – 12
= -4.

5) Comme (v_n) est géométrique, on utilise la formule explicite (qui dépend de n),
v_n = v_p×q^n-p avec p = 0 comme on commence à 0.

Du coup, pour tout n, v_n
= v₀×qⁿ = -4×0,85ⁿ.

Comme v_n = u_n – 12,
alors u_n = v_n + 12
= -4×0,85ⁿ + 12
= 12 – 4×0,85ⁿ.

6) Pour obtenir le sens de variation d’une suite, il faut déterminer le signe de
u_n+1 – u_n. S’il est positive, la suite est croissante. S’il est négatif, la suite est décroissante.

Pour tout n réel, u_n+1 – u_n
= 12 – 4×0,85ⁿ⁺¹ – [12 – 4×0,85ⁿ] (on n’oublie pas les crochets après le “moins”)
= 12 – 4×0,85ⁿ⁺¹ – 12 + 4×0,85ⁿ (les 12 s’annulent)
= – 4×0,85ⁿ⁺¹ + 4×0,85ⁿ
= 4×0,85ⁿ – 4×0,85ⁿ⁺¹
= 4×[ 0,85ⁿ – 0,85ⁿ⁺¹ ] (on factorise par 4)
= 4×[ 0,85ⁿ – 0,85ⁿ × 0,85 ] (les puissances : aⁿ⁺¹ = aⁿ × a¹ = aⁿ × a)
= 4×[ 0,85ⁿ × 1 – 0,85ⁿ × 0,85 ]
= 4×[ 0,85ⁿ × (1 – 0,85) ] (on factorise par 0,85ⁿ)
= 4×[ 0,85ⁿ × 0,15 ].

4 est positif, 0,85ⁿ est positif, 0,15 est positif. D’après la règle des signes avec ce produit,
Pour tout n réel, u_n+1 – u_n > 0.
Donc la suite (u_n) est strictement croissante.

7) u_n = 12 – 4*0,85ⁿ
lim_n→+∞ 0,85ⁿ = 0 car 0 < 0,85 < 1,
Par produit, lim_n→+∞ 4×0,85ⁿ = 0 car 4*0,

Par somme, lim_n→+∞ (12 – 4×0,85ⁿ) = 0 car 12-0,

Donc la limite de la suite est 12.

8) On prend le nombre actuel d’abonnés u_n, on lui applique une baisse de 15% (coefficient multiplicateur de 0,85) donc on obtient 0,85×u_n.
Puis on ajoute 1800, soit 1,8 millier, cela donne 0,85×u_n + 1,8.
On obtient le nombre suivant d’abonnés qui est u_n+1.
Du coup, on a pour tout n entier naturel u_n+1 = 0,85×u_n + 1,8.
Sans oublier que u₀ = 8, ce qui correspond au 8000 de 2008.
Cette situation peut donc être modélisée par la suite (u_n).

9) 2014, c’est 2008+6 soit 2008+n pour n=6.
Il faut donc calculer
u₆ = 12 – 4×0,85⁶ = 10,4914, soit un nombre d’abonnés de 10491 en 2014.