Exercice : Clic droit vers l’exercice
Tout le corrigé :
1) Voici le dessin de la pyramide :
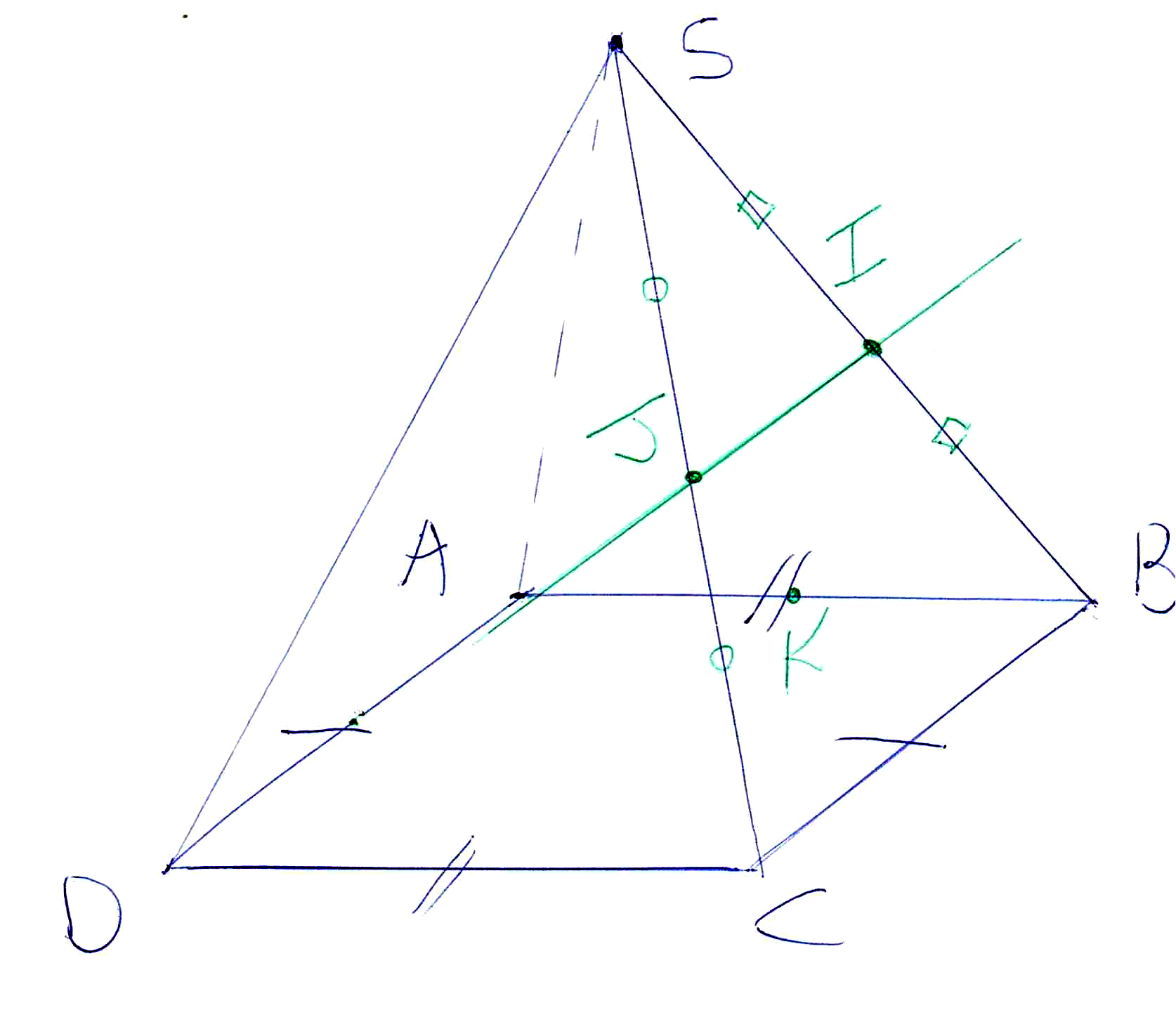
I est le milieu de [SB], J est le milieu de [SC]. D’après le théorème de la droite des milieux, (IJ) // (BC).
On sait aussi que ABCD est un parallélogramme
donc (AD) // (BC).
Or, deux droites parallèles à une même troisième droite (ici (BC)) sont parallèles entres elles, donc (IJ) // (AD).
2) Voici le dessin du plan (SDK) :
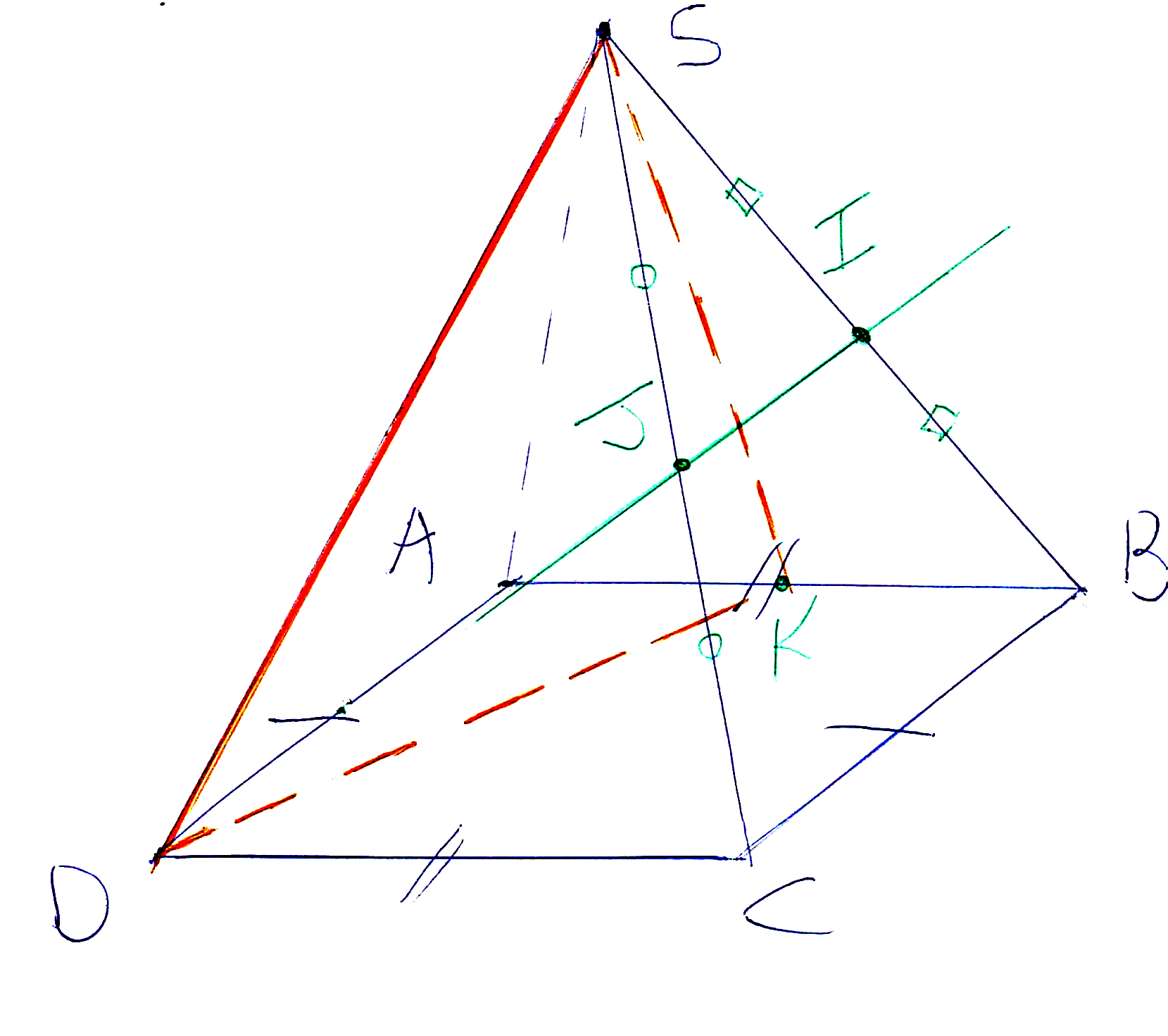
Comme (IJ) est parallèle à (AD), alors (IJ) est parallèle à tout plan contenant (AD) comme (SDA). Donc (IJ) // (SDA).
Or (SDA) et (SDK) sont sécants en (SD) car cette droite est commune aux deux plans et ils ne sont pas confondus.
Il est clair que (SD) n’est pas parallèle à (IJ) car (IJ)//(AD).
Raisonnement par l’absurde :
On sait que (IJ) // (SDA) et on suppose (IJ) // (SDK).
Si une droite est parallèle à deux plans et,
si ces deux plans sont sécants,
alors leur intersection (ici (SD)) est une droite parallèle à la droite en question (ici (IJ)) :
soit (IJ) // (SD).
Or on n’a vu plus haut que ce n’est pas le cas : donc (IJ) ne peut pas être parallèle à (SDK).
Donc (SDK) et (IJ) sont sécants.
3) L’intersection de deux plans sécants est une droite. Il faut donc trouver deux points qui sont à la fois sur (SDK) et (SBC). On a déjà le point S d’après de le nom des plans.
Quand on regarde la figure, on voit que (DK) et (BC) sont sur un même plan, celui du “sol”.
La droite (DK) appartient au plan (SDK) et la droite (BC) appartient au plan (SBC) d’après les noms.
De plus, (DK) et (BC) sont sécantes : elles ont donc un point d’intersection qui appartient aux deux droites. Du coup, ce point d’intersection appartient aux deux plans (SDK) et (SBC).
Pour le tracer, il suffit de prolonger les droites assez loin.
Voici le dessin du prolongement des droites et du point d’intersection :
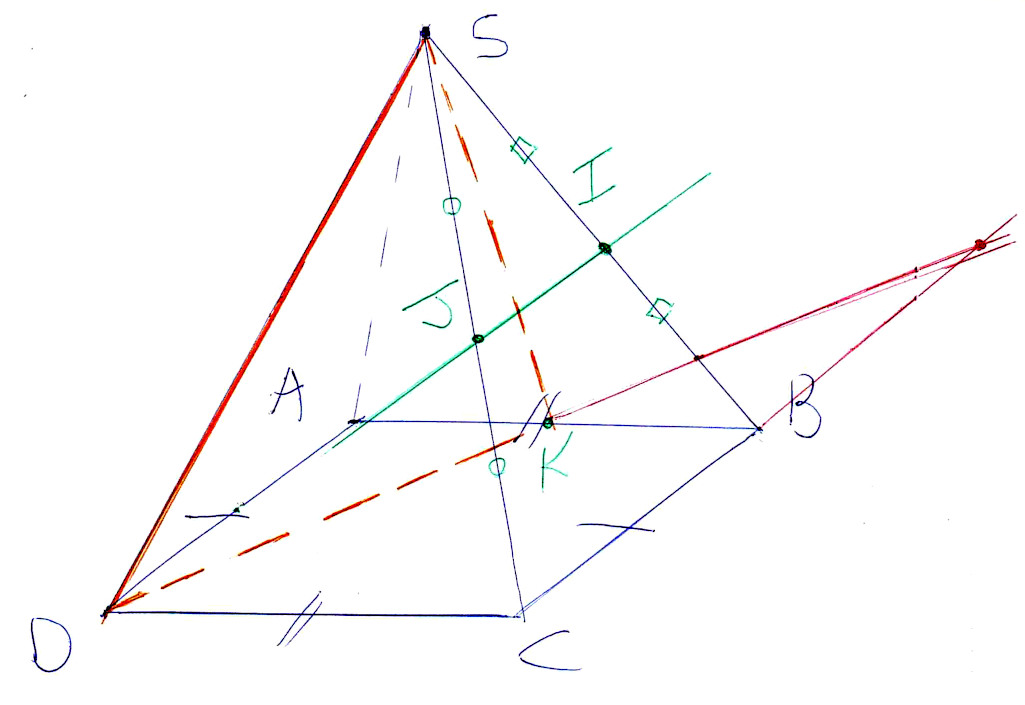
Avec ces deux points (S et ce dernier), on a la droite d’intersection. Il suffit de la tracer.
4) On sait que (IJ) et (SKD) sont sécant d’après la question 1).
On connait l’intersection du plan (SBC) avec (SDK). C’est la droite rouge.
Or la droite (IJ) appartient à la face -au plan- (SBC), donc son intersection avec (SKD) sera sur la droite rouge.
Voici le dessin de la droite rouge et du point d’intersection de (IJ) et (SDK) :
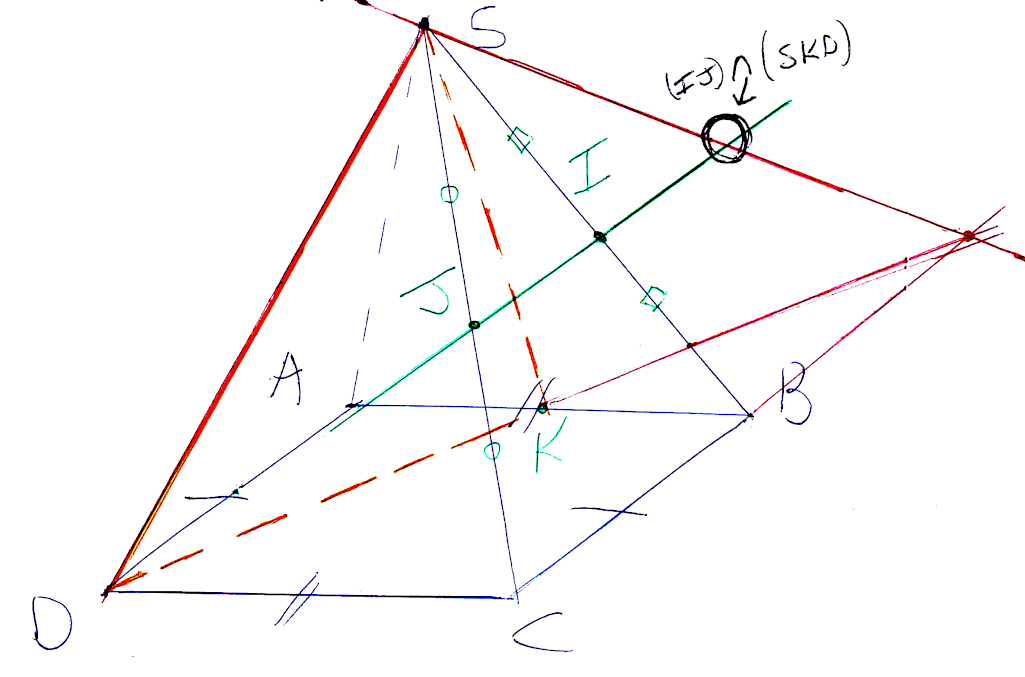
Je justifie ci-dessous :
L’intersection de deux droites sécantes est un point. En prolongeant (IJ) vers la droite rouge, on trouve le point d’intersection (en noir) de (IJ) et de cette droite, soit l’intersection de (IJ) et de (SKD).

