Exercice : Clic droit vers l’exercice
Tout le corrigé :
1) L’effectif de la classe [17 ; 19[ est égal à 2. La surface des rectangles verticaux est proportionnelle à l’effectif de la tranche.
La surface est ici de 2 x 2 (largeur de la classe fois la hauteur). On a donc une surface de 4 pour un effectif de 2. La conséquence ici est que l’effectif fait 2 fois moins que la surface.
Pour la classe [4 ; 10[, on a une surface de 3×6 soit 18. Donc ici, l’effectif est de 9 car 2 fois moins que la surface.
Pour la classe [10 ; 12[, on a une surface de 5×2 soit 10. Ici, l’effectif est de 5 car 2 fois moins que la surface.
Pour la classe [12 ; 15[, on a une surface de 6×3 soit 18. Ici, l’effectif est de 9 car 2 fois moins que la surface.
Pour la classe [15 ; 17[, on a une surface de 5×2 soit 10. Ici, l’effectif est de 5 car 2 fois moins que la surface.
Pour la classe [19 ; 29[, on a une surface de 1×10 soit 5. Ici, l’effectif est de 5 car 2 fois moins que la surface.
2) Dans le premier échantillon, il y a un effectif N de 40.
Pour obtenir le premier quartile Q1, il faut prendre la valeur de l’élément avec le numéro N/4 (ou le premier entier au-dessus de ce nombre).
Ici 40/4 = 10 donc on prend la 10ème valeur qui vaut
Q1 = 262 pour la première série.
Cela veut dire que 25% des valeurs sont inférieures ou égales à 262.
Pour la seconde série, 36/4 = 9 donc on prend la 9ème valeur qui vaut
Q1 = 267.
Donc 25% des valeurs sont inférieures ou égales à 267.
Pour calculer Q3, c’est l’élément numéro 3N/4 (ou le premier entier au-dessus de ce nombre) qu’il faut prendre puis donner sa valeur.
Soit 3×40/4 le 30ème pour la seconde série :
Q3 = 266.
Pour la première série, 75% des valeurs sont inférieuresou égales à 266.
Soit 3×36/4 le 27ème pour la seconde série :
Q3 = 272.
Pour la première série, 75% des valeurs sont inférieuresou égales à 272.
3) L’intervalle interquartile se calcule en faisant
Q3 – Q1.
Il vaut 266 – 262 = 4 pour la série 1.
Il vaut 272 – 267 = 5 pour la série 2.
Selon cet indicateur, les valeurs de la seconde série sont plus dispersées.
4) Pour le diagramme en boîte, il faut faire un rectangle qui commence à Q1 à gauche et qui finit à Q3 à droite.
Sur les côtés du rectangle, on trace deux traits horizontaux qui vont vers le minimum et le maximum à partir du rectangle. On met un gros point sur ces valeurs.
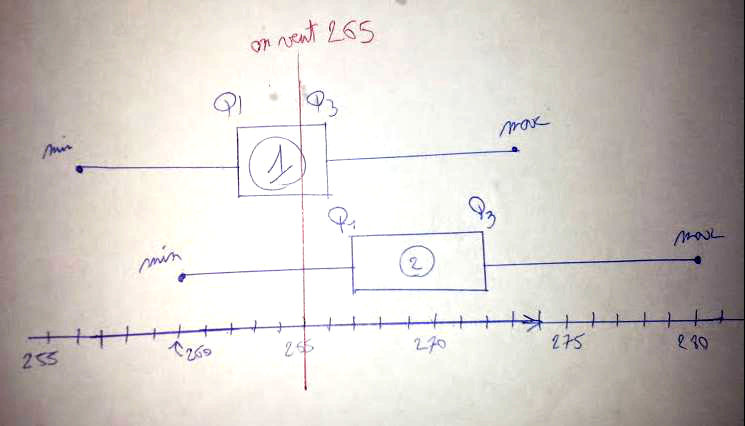
5) D’après la diagramme ci-dessus, la machine qui semble la plus appropriée est celle dont la boîte (le rectangle) se resserre autour de la valeur médiane voulue, soit 265. C’est donc la première machine pour laquelle la boîte Q1/Q3 contient la médiane Me = 265.
6) La moyenne d’une série statistique est :
Faisons un tableau d’effectifs avec les valeurs de la second série :

La moyenne est donc d’environ 269,9722 soit environ 269,97 à 0.01 près.
La variance indique la dispersion des valeurs autour de la moyenne. Sa formule est :
V = ( n1(x1 – –x)² + n2(x2 – –x)² + … + nP(xP – –x)² ) / (n1 + n2 + … + nP)
J’ai donc calculé le numérateur avec ce grand tableau.

D’abord, je calcule les carrés des différences en passant de gauche à droite. Ensuite, je calcule la somme totale du numérateur.
Enfin, j’obtiens la variance en divisant le numérateur 766.9724 par l’effectif total 40.
Cela donne V = 766.9724/40 = 21.3048 environ.
Un calculateur internet (ou votre calculatrice) me retourne une variance de 21.9135. Il a surement considéré une moyenne de 269,9722 (quatre chiffres après la virgule) alors que j’ai utilisé 269,97 (deux chiffres après la virgule) pour expliquer le calcul à la main avec les 18 lignes.
Si le nombre de lignes de calcul est de 5 ou 10, il vaut donc mieux utiliser 4 chiffres après la virgule pour la précision de la moyenne.
L’écart-type σ est la racine de la variance. Il indique aussi à quel point les valeurs sont dispersées. On utilise la racine car on avait mis des carrés pour la variance.
σ = √V
σ = √21.3048
σ = 4.6157 environ.
L’écart-type calculé est d’environ 4.6157.
Le calculateur internet (ou votre calculatrice) me retourne un écart-type de 4.6812. Il a surement considéré une moyenne de 269,9722 (quatre chiffres après la virgule) alors que j’ai utilisé 269,97 (deux chiffres après la virgule) pour expliquer le calcul à la main avec les 18 lignes.
Si le nombre de lignes de calcul est de 5 ou 10, il vaut donc mieux utiliser 4 chiffres après la virgule pour la précision de la moyenne.
Bonne compréhension,
Sylvain Jeuland

