frenchmaths.com (par Sylvain Jeuland)

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) La dérivée de e^u(x) est u ‘ (x)×e^u(x).
Cela veut dire qu’on dérive ce qu’il y a en haut de l’exponentielle puis on la place devant en coefficient multiplicateur.

La dérivée de x est 1. Donc e^x se dérive en 1×e^x.

La dérivée de 2x est 2. Donc e^2x se dérive en 2×e^2x.

On a f(x) = 2×e^x – e^2x.

Donc f ‘ (x) = 2×1×e^x – 2×e^2x
= 2e^x – 2e^2x

2) On doit partir de notre forme développée (avec un “moins” au milieu) vers une forme factorisée avec un produit de deux facteurs, qui sont 2e^2x et la parenthèse (1 – e^x).

Tout d’abord, e^2x = (e^x)².

Pour prouver une égalité, il est pratique de partir d’un côté du “égal” et arriver à l’autre membre de l’autre côté du “égal”. Développons le membre de droite pour retrouver celui de gauche (sans écrire f ‘ (x)).

2×e^x(1 – e^x)
= 2×e^x×1 – 2×e^x×e^x
= 2×e^x – 2×(e^x)².
= 2×e^x – 2×e^2x
= f ‘ (x)
d’après la dérivée de la question 1).

On a bien f ‘ (x) = 2×e^x(1 – e^x).

3) Pour obtenir les variations de la fonction f sur R, étudions le signe de f ‘ (x). Pour cela, on utilise la forme factorisée pour faire le tableau de signe suivant.

Nous dévons résoudre l’inéquation 1 – e^x ≥ 0 pour déterminer pour quelles valeurs de x cette expression est positive, on pourra mettre un + pour ces valeurs de x.
1 – e^x ≥ 0
⇔ -e^x ≥ -1
⇔ e^x ≤ 1 (On change le sens de l’inégalité car on divise par le nombre négatif -1 de chaque côté.)
⇔ e^x ≤ e⁰
⇔ x ≤ 0 (car la fonction exponentielle est strictement croissante sur R.)
⇔ x ∈ ]-∞ ; 0]
Soit x à gauche de zéro. On met donc le + à gauche de la valeur x = 0 dans le tableau de signe.

Voici le tableau de signe de f ‘ (x) puis le tableau de variation de f :

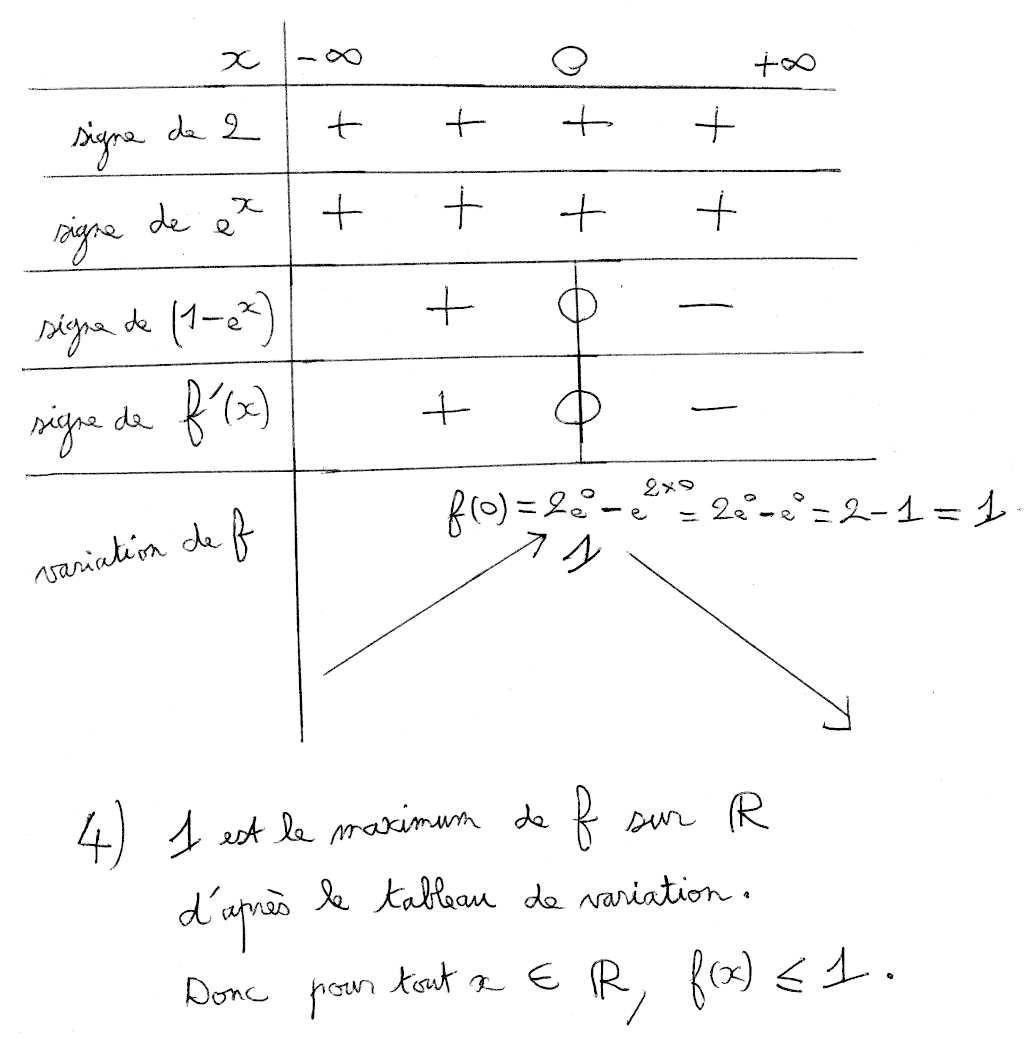
5) La dérivée de e^u(x) est u ‘ (x)×e^u(x).
Cela veut dire qu’on dérive ce qu’il y a en haut de l’exponentielle puis on la place devant en coefficient multiplicateur.

La dérivée de x est 1. Donc e^x se dérive en 1×e^x.

La dérivée de 3x est 3. Donc e^3x se dérive en 3×e^3x.

On a g(x) = 3×e^x – e^3x.

Donc g ‘ (x) = 2-3×1×e^x – 2-3×e^2-3x
= 3e^x – 3e^3x

6) On doit partir de notre forme développée (avec un “moins” au milieu) vers une forme factorisée avec un produit de deux facteurs, qui sont 3e^3x et la parenthèse (1 – e^x).

Tout d’abord, e^3x = (e^x)³.

Pour prouver une égalité, il est pratique de partir d’un côté du “égal” et arriver à l’autre membre de l’autre côté du “égal”. Développons le membre de droite pour retrouver celui de gauche (sans écrire g ‘ (x)).

3×e^x(1 – e^x)
= 3×e^x×1 – 3×e^x×e^x
= 3×e^x – 3×(e^x)³.
= 3×e^x – 3×e^2x
= g ‘ (x)
d’après la dérivée de la question 1).

On a bien g ‘ (x) = 3×e^x(1 – e^x).

7) Pour obtenir les variations de la fonction g sur R, étudions le signe de g ‘ (x). Pour cela, on utilise la forme factorisée pour faire le tableau de signe suivant.

Nous dévons résoudre l’inéquation 1 – e^2x ≥ 0 pour déterminer pour quelles valeurs de x cette expression est positive, on pourra mettre un + pour ces valeurs de x.
1 – e^2x ≥ 0
⇔ -e^2x ≥ -1
⇔ e^2x ≤ 1 (on change le sens de l’inégalité car on divise par le nombre négatif -1 de chaque côté)
⇔ e^2x ≤ e⁰
⇔ 2x ≤ 0 (car la fonction exponentielle est strictement croissante sur R.)
⇔ x ≤ 0 (On ne change pas le sens de l’inégalité quand on divise par un nombre positif (ici 2) de chaque côté.)
⇔ x ∈ ]-∞ ; 0]
Soit x à gauche de zéro. On met donc le + à gauche de la valeur x = 0 dans le tableau de signe.

Voici le tableau de signe de g ‘ (x) puis le tableau de variation de g :

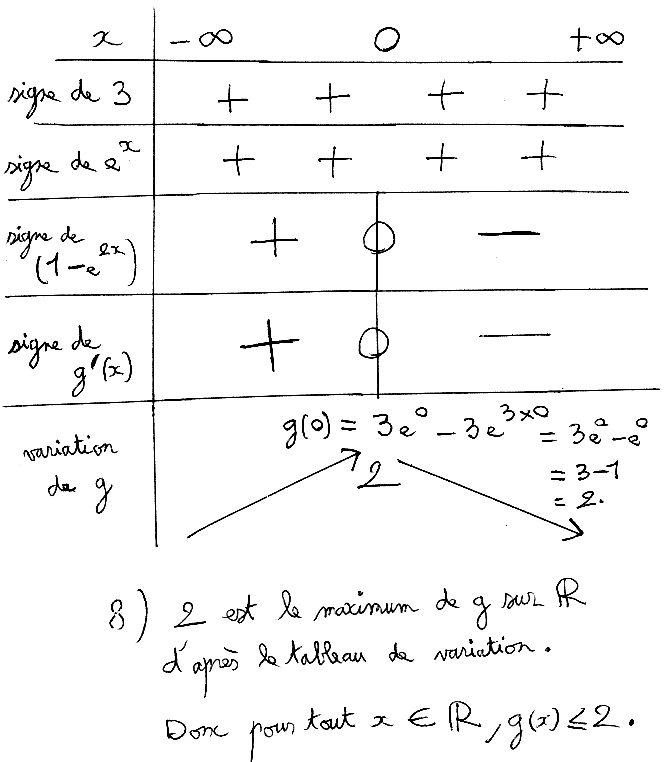
Bonne compréhension,
Sylvain Jeuland