Exercice : Clic droit vers l’exercice
Tout le corrigé :
1) Pour obtenir la valeur estimée du taux en 2009, on voit que la petite croix sur le graphique au dessus de l’abscisse 9 correspond à 2009, donc on calcule f(9).
f(9) = −0,04 × 93 + 0,68 × 92 − 0,06 × 9 + 51,4
= 76.78.
2) Pour calculer un pourcentage d’erreur, on utilise la formule suivante :
[(ValeurMesurée – ValeurEstimée)/(ValeurMesurée)] × 100
= [(75.7 – 76.78)/(75.7)] × 100
= [(– 1.08)/(75.7)] × 100
= -1.427 environ.
Le pourcentage d’erreur est de 1.43%.
3) On a f(x) = −0,04x3 + 0,68x2 − 0,06x + 51,4 donc
f'(x) = −0,04 × 3x2 + 0,68 × 2x − 0,06 × 1 + 0
= −0,12x2 + 1,36x – 0,06
Pour obtenir les variations de f, on a besoin du signe de f ‘ (x).
C’est un polynôme du second degré.
Δ = b2 – 4ac
= 1.362 – 4 × (-0,12) × (-0,06)
= 1.8496 – 0.0288
= 1.8208 > 0
donc ce polynôme a deux racines réelles.
x1 = (-b – √Δ)/(2a)
= (-1.36 – √1.8208)/(2(−0,12))
= 11.289 environ
x2 = (-b + √Δ)/(2a)
= (-1.36 + √1.8208)/(2(−0,12))
= 0.0443 environ
On obtient le tableau de signe de f ‘ (x) et de variation de f suivant :
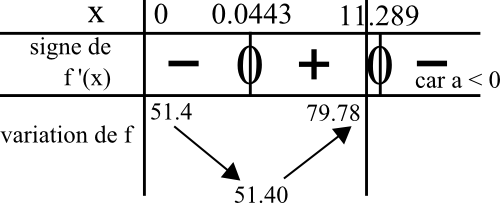
Je vais de -∞ à +∞ pour faire le signe du polynôme du second degré, puis je coupe à 0 et 11 pour coller au domaine de définition. Je calcule aussi f(0), le minimum, puis f(11).
4) On a f ‘ (x) = −0,12x2 + 1,36x – 0,06
donc
f’ ‘ (x) = −0,12 × 2x + 1.36 + 0
= -0.24x + 1.36.
Pour obtenir la convexité de f, on a besoin du signe de f ‘ ‘ (x) (on peut intercaler les variations de f ‘).
On met un + dans la ligne de -0.24x + 1.36
⇔ -0.24x + 1.36 ≥ 0
⇔ -0.24x ≥ -1.36
⇔ -0.24x/(-0.24) ≤ -1.36/(-0.24)
⇔ x ≤ 17/3
⇔ à gauche de 17/3
On met donc le + à gauche dans la ligne de -0.24x + 1.36.
On obtient le tableau de signe de f ‘ ‘( x), de variation de f ‘, de convexité de f suivant :
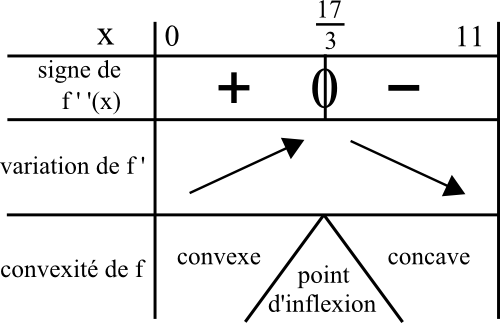
5) D’après le tableau de convexité de f, f passe de convexe à concave au point d’abscisse 17/3. Donc f admet un point d’inflexion en cette abscisse.
L’équation d’une tangente à courbe Cf au point d’abscisse a est :

Je vais calculer les valeurs approchées de f(17/3) et de f ‘ (17/3).
f(17/3) = 65.617
f ‘ (17/3) = 3.793
Donc y = 3.793 × (x – 17/3) + 65.617
y = 3.793x – 3.793 × 17/3 + 65.617
y = 3.793x + 44.123
C’est l’équation de la tangente au point d’inflexion avec des valeurs approchées.
6) Comme la fonction passe de convexe à concave en ce point d’inflexion, cette tangente est en dessous de C avant 17/3, puis au dessus de C après 17/3.
Je trace ci-dessous la courbe et la tangente pour x allant de 0 à 11 (carreaux de 1 en 1) et y allant de 0 à 90 (carreaux de 10 en 10).
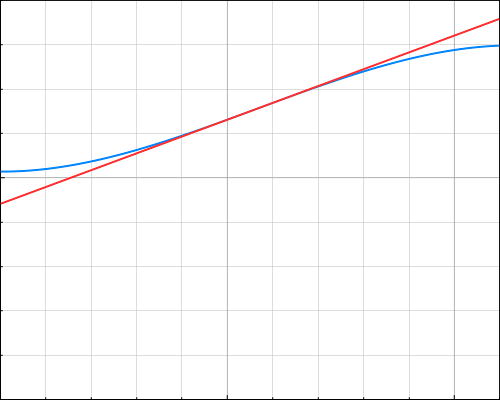
7) La diminution du rythme de croissance du taux d’endettement, c’est quand la fonction passe de convexe à concave, c’est à dire au niveau du point d’inflexion, que le rythme de croissance commence à diminuer. Pour 17/3, soit 5+(2/3). C’est à partir des deux-tiers de 2005 que ce rythme diminue.
Bonne compréhension,
Sylvain Jeuland

