Exercice : Clic droit vers l’exercice
Tout le corrigé :
1) Pour calculer la mesure d’un principale d’un angle, l’idéal est de mettre 2π sous la forme d’une fraction avec le même dénominateur que notre angle.
2π = 6π/3
La mesure principale doit se situer dans l’intervalle ]-π ; π]. Là aussi, l’idéal est de mette les π sous la forme d’une fraction avec le même dénominateur que notre angle.
]-π ; π] = ]-3π/3 ; 3π/3].
Si l’angle de départ est au delà de l’intervalle ]-π ; π], il faut enlever les 2π jusqu’à l’atteindre.
Si l’angle de départ est en deçà de l’intervalle ]-π ; π], il faut ajouter les 2π jusqu’à l’atteindre.
Du coup, comme j’ai tout mis sur le même dénominateur et qu’il y a des π partout, on peut partir de -11 (pour -11Π/3), ajouter plusieurs fois 6 (pour 6π/3) pour arriver dans l’intervalle ]-3 ; 3] (pour ]-3π/3 ; 3π/3]).
-11 + 6 = -5
-5 + 6 = 1
1 appartient bien à ]-3 ; 3] donc la mesure principale est 1Π/3.
Pour les deux autres angles, on fait de même et on obtient 1Π/4 et 5Π/6.
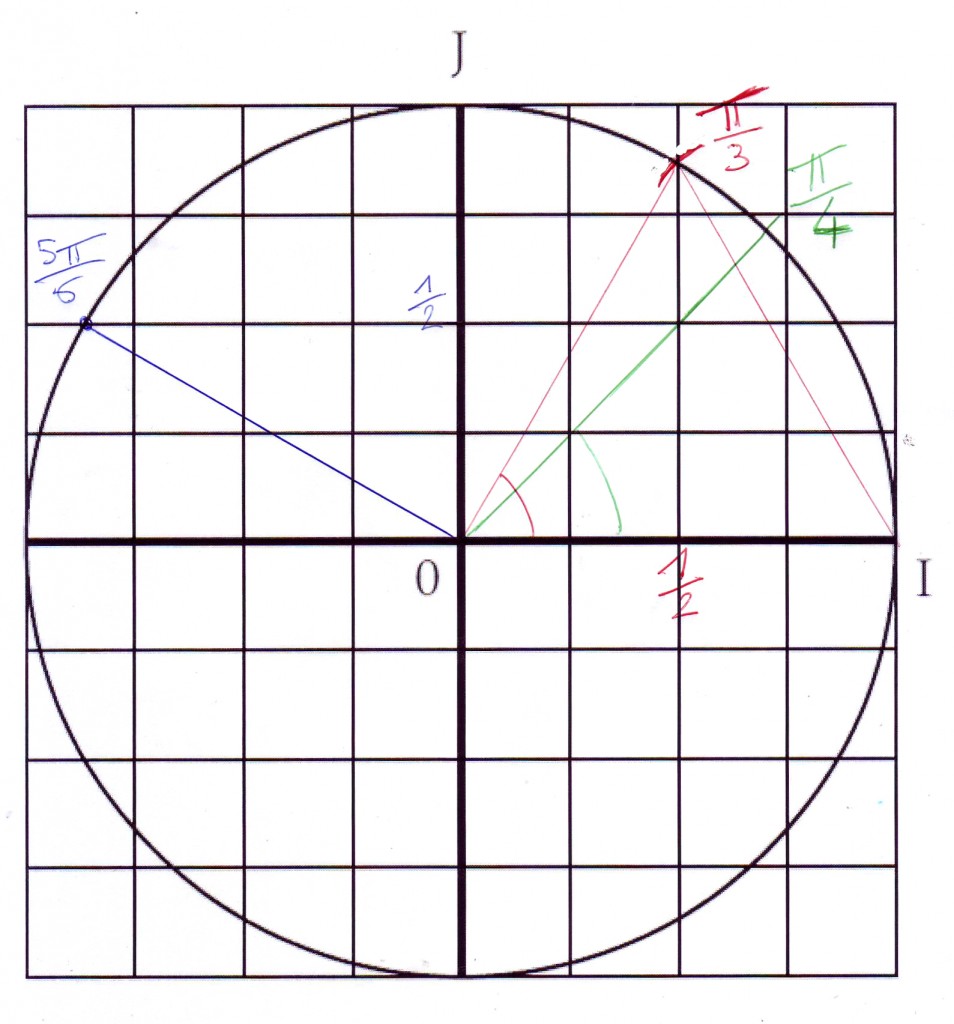
2) Pour déterminer les placements des angles 4Π/3, 3Π/4 et Π/6, il faut penser à des gâteaux.
Un gâteau avec des parts de Π/3 est un gâteau avec un découpage pour 6 personnes.
Un gâteau avec des parts de Π/4 est un gâteau avec un découpage pour 8 personnes.
Un gâteau avec des parts de Π/6 est un gâteau avec un découpage pour 12 personnes.
Déjà, détermine la taille d’une part à partir de la gauche (l’angle 0), puis ajoute le nombre de parts de même taille pour arriver au bon angle.
Pour Π/3, vas jusqu’à 1 part d’un gâteau de 6 personnes.
Pour Π/4, vas jusqu’à 1 part d’un gâteau de 8 personnes.
Pour 5Π/6, vas jusqu’à 5 parts d’un gâteau de 6 personnes.
3-4-5) On a :
(→u ; →v) = –Π/9 et
(→u ; →w) = Π/4.
3) (→v, →w) :
Comme on connaît →u et →v donc on peut faire Chasles entre →v et →w en plaçant →u au milieu.
(→v, →w)
= (→v, →u) + (→u, →w).
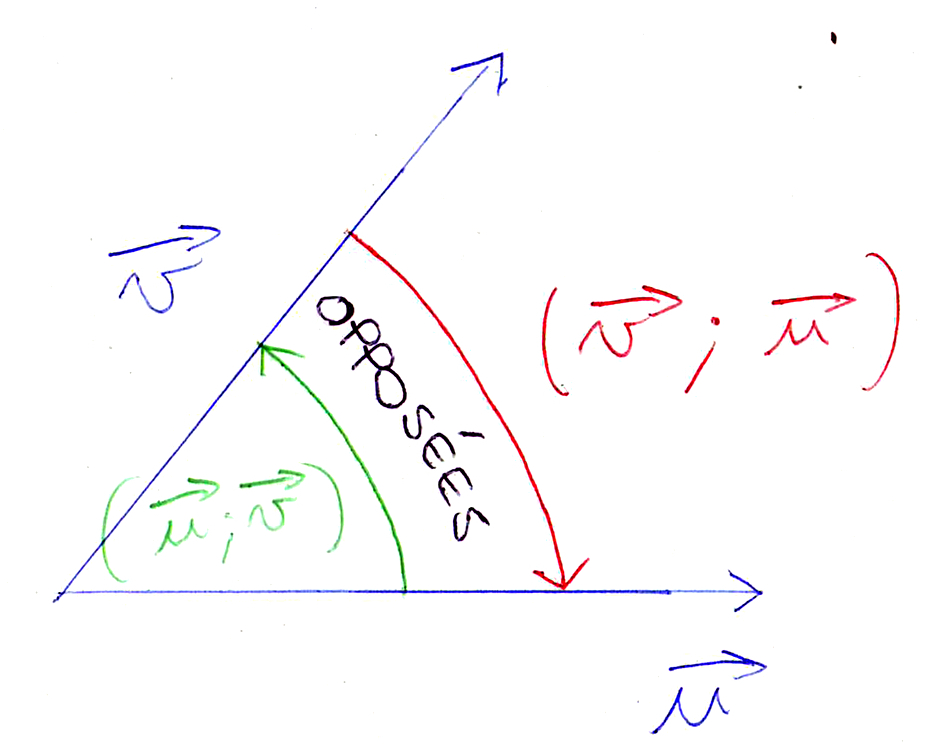
(→v, →u) se calcule en inversant le sens de
(→u, →v) car si on va de →v vers →u, c’est en sens contraire de →u vers →v.
Donc :
(→v, →u) = -(→u, →v).
(→v, →w)
= (→v, →u) + (→u, →w)
= -(→u, →v) + (→u, →w)
= -(-Π/9) + Π/4
= 4Π/36 + 9Π/36
= 13π/36.
4) (-→u ; →v) :
Lorsqu’on a “un seul moins” devant un vecteur, cela renverse ce vecteur vers l’autre sens donc il se crée un demi-tour, soit un changement d’angle de π. Dans le schéma ci-dessous les deux vecteurs ->u et ->v sont inversés.
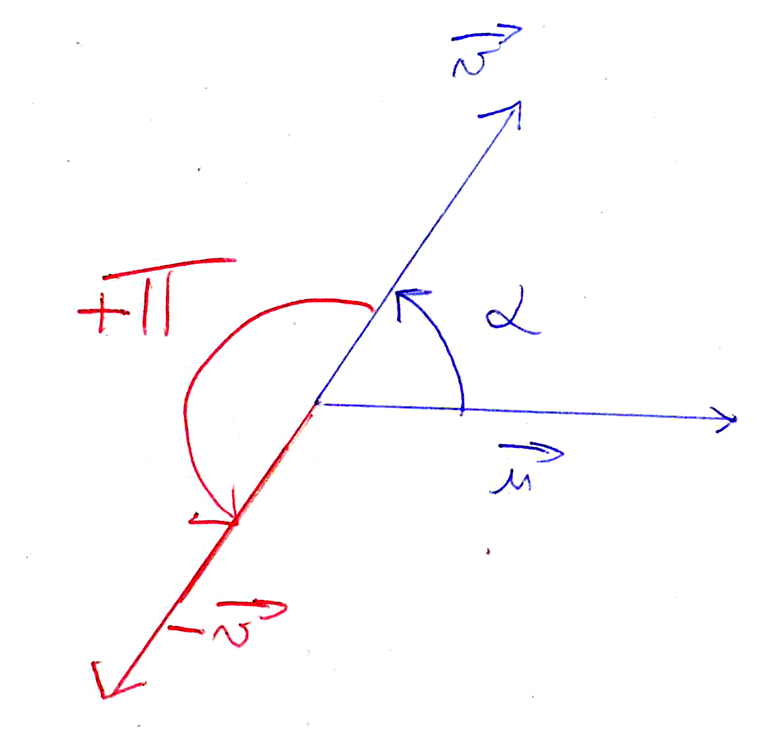
On a donc : (-→u, →v)
= (→u, →v) + π
= –Π/9 + π
= 8π/9
5) (-2→u ; →w).
Ici, c’est pareil, c’est le signe “moins” qui compte devant, la valeur “2” ne change rien. Du coup, on fait +π aussi.
On a donc : (-2→u, →w)
= (→u, →v) + π
= Π/4 + π
= 5π/4
= -3π/4 (mesure principale en enlevant 2π).

