Exercice : Clic droit vers l’exercice
Tout le corrigé :
Dessinons l’arbre de probabilité avec les données de l’exercice en vert. Comme la probabilité qu’il gagne la première partie est de 0,1, je mets 0,1 vers p(G1) et
1 – 0,1 = 0,9 vers p(–G1).
S’il gagne une partie, la probabilité de gagner la suivante est égale à 0,8. Du coup, c’est un SACHANT et on le mets après la condition du “sachant” (sur une branche de droite). Comme la condition est de gagner la première partie, on met le 0,8 à droite du p(G1) vers la probabilité de gagner la seconde partie soit p(G2 ⋂ G1) (on a gagné à la fois la 1ère et la 2ème partie).
Et du coup, on met le 1 – 0,8 = 0,2 juste en dessous.
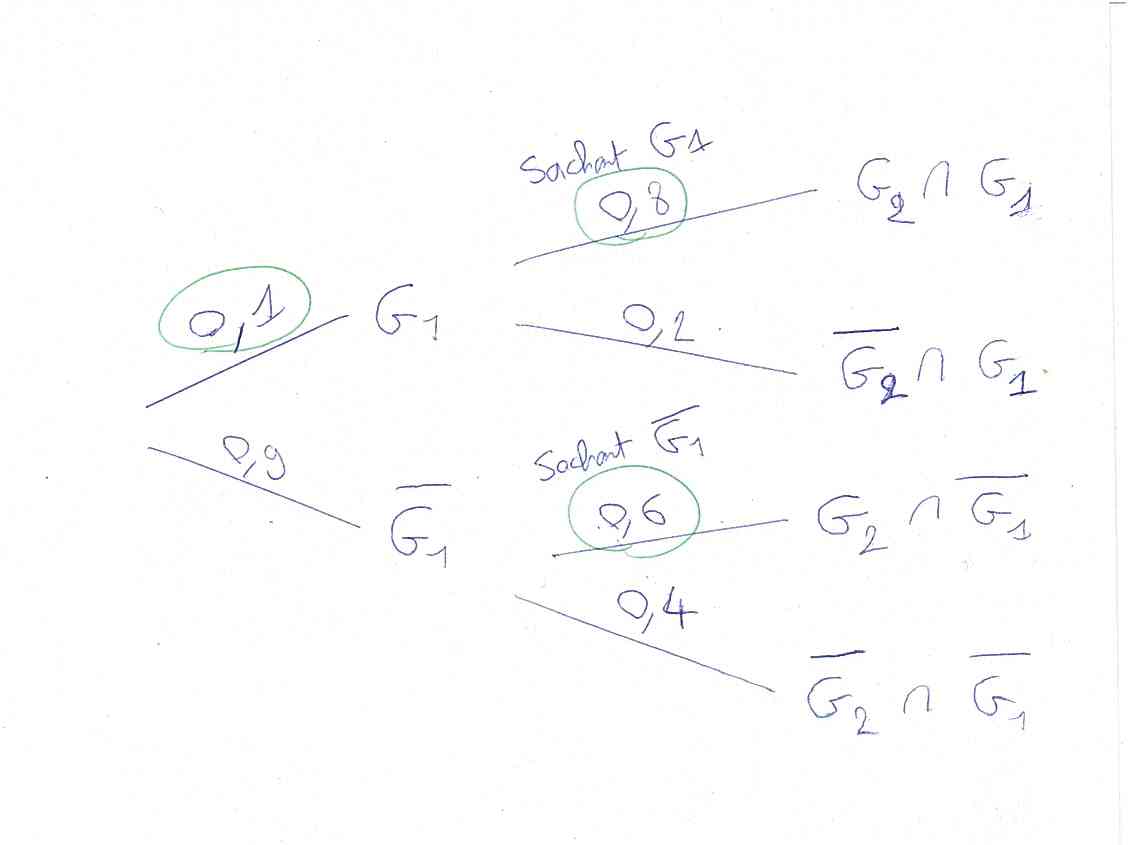
On fait de même avec la probabilité de gagner la 2ème partie si on a perdu la première. On est encore dans un SACHANT mais cette fois “sachant” P(–G1) car on a perdu la première partie. On place donc le 0,6 après le P(–G1) vers la seconde victoire qui est P(G2 ⋂ –G1) car on a à la fois perdu la 1ère et gagné la seconde. En dessous, on fait 1 – 0,6 = 0,4.
1) On veut maintenant calculer P(G2). On voit que le G2 apparaît dans G2 ⋂ G1 et G2⋂–G1. Pour arriver à G2, on doit donc passer par G1 ou –G1.
La rédaction est :
G1 et –G1 forment une partition de l’univers Ω.
D’après la Formule des Probabilités Totales,
P(G2) = P(G2 ⋂ G1) + p(G2 ⋂ –G1)
= P(G1) × P(G2 ⋂ G1) + p(–G1) × P(G2 ⋂ –G1)
= 0,1 × 0,8 + 0,9 × 0,6 en lisant de gauche à droite (avec les “sachants” à droite).
= 0,08 + 0,54 = 0,62.
2) “Le joueur a gagné la deuxième partie. Calculer la probabilité qu’il ait perdu la première.”
Cela veut dire qu’on SAIT qu’on est en G2 et on veut –G1.
Donc cela revient à calculer P(–G1 sachant G2)
= P(–G1 ⋂ G2)/P(G2)
= (0,9 × 0,6)/0,62 = 0,871.
On a donc PG2(–G1) = 0,871.
3) Pour gagner au moins une partie sur les trois premières, il faut arriver dans l’un de ces trois cas :
– Gagner la 1ère (G1, peu importe les autres).
– Perdre la 1ère et gagner la 2ème (–G1 ⋂ G2), peu importe la dernière.
– Perdre les deux premières et gagner la 3ème (–G1 ⋂ –G2 ⋂ G3).
Cela revient à faire cet arbre :
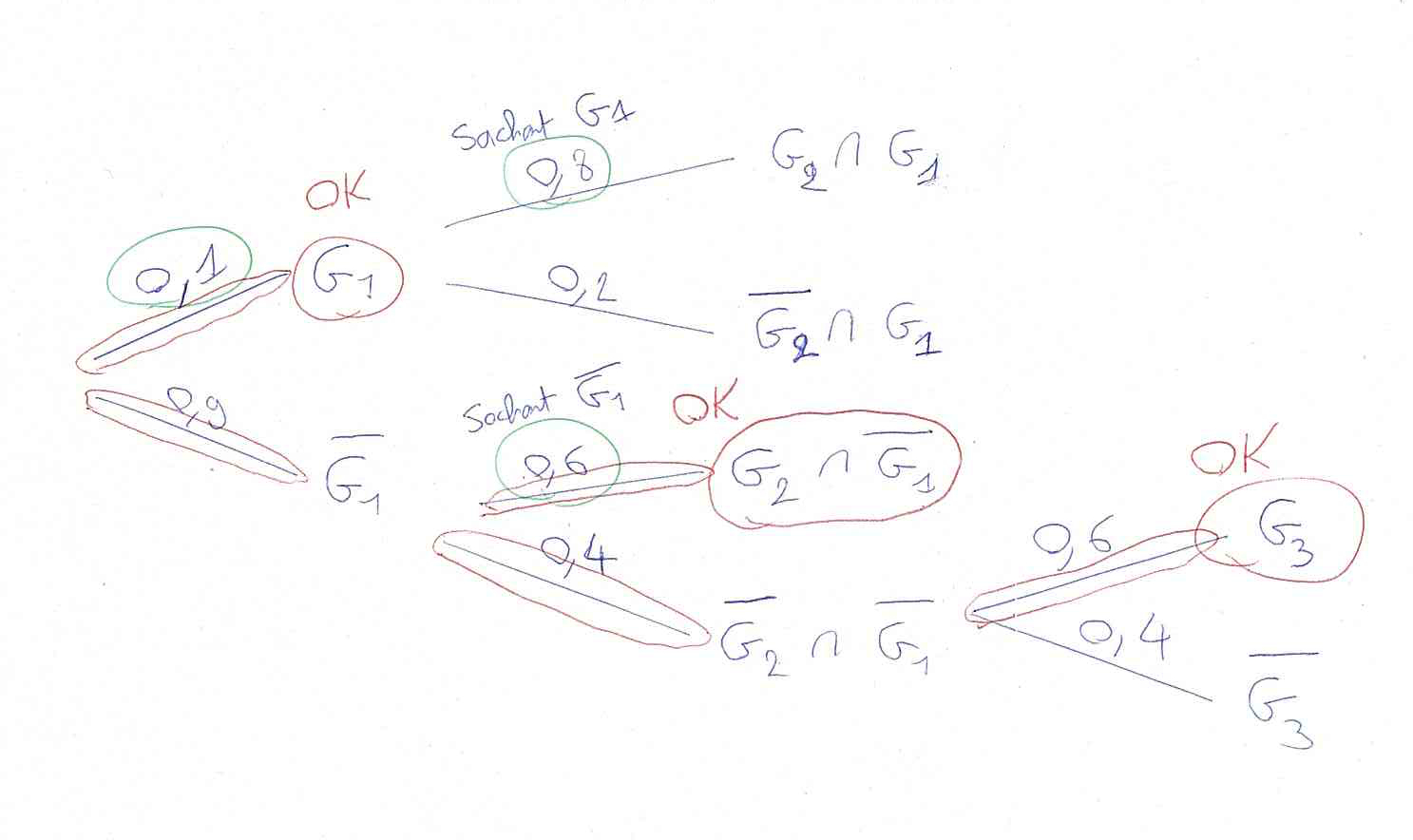
On calcule donc :
P(gagner au moins une partie sur les trois)
= 0,1 + 0,9 × 0,6 + 0,9 × 0,4 × 0,6
= 0,64 + 0,216
= 0,856.
4) Pour démontrer cette formule à l’étape n+1 en fonction de l’étape n, il faut dessiner le passage de la partie n à la partie n+1 dans l’arbre de probabilité. Tout d’abord, représente les probabilités de gagner et perdre la partie n à gauche :
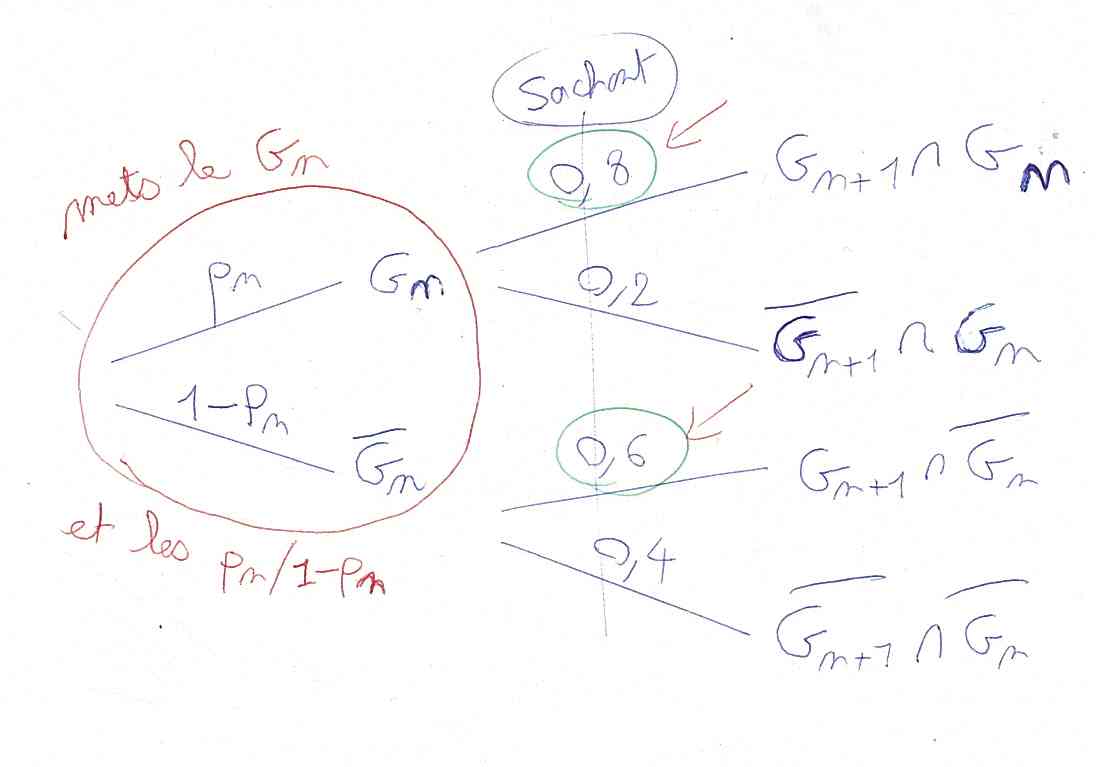
Tu peux voir tout à droite que pour avoir P(Gn+1), tu as besoin des ⋂ Gn et ⋂ –Gn. Une fois de plus, on utilise la Formule des Probabilités Totales comme ci-dessous :
Gn et –Gn forment une partition de l’univers Ω.
D’après la Formule des Probabilités Totales,
pn+1
= P(Gn+1)
= P(Gn+1 ⋂ Gn) + P(Gn+1 ⋂ –Gn)
= pn × 0,8 + (1 – pn) × 0,6
= 0,8pn + 0,6 – 0,6pn
= 0,2pn + 0,6
= (1/5)pn + 3/5.
car 0,2 = 1/5 et 0,6 = 3/5.
5) Pour obtenir un raisonnement par récurrence, il faut utiliser au moins une donnée. Dans le 4) on a démontré que
pn+1 = (1/5)pn + 3/5.
Je dois prouver que
pn = 3/4 − (13/4) × (1/5)n.
Je commence par l’initialisation avec n = 1 :
D’une part, p1 = 0,1.
D’autre part,
3/4 − (13/4) × (1/5)1
= 3/4 – 13/20
= 15/20 – 13/20
= 2/20
= 0,1.
On a bien p
La propriété est vraie au rang 1.
Je dois maintenant faire l’hérédité :
Pour cela, je SUPPOSE que la propriété est vraie au rang n, puis je dois PROUVER qu’elle est vraie au rang n+1.
La supposition devient donc une DONNÉE au sein même de l’hérédité.
On a donc comme données :
pn+1 = (1/5)pn + 3/5 (donnée permanente),
pn = 3/4 − (13/4) × (1/5)n. (donnée supposée).
On doit donc arriver à la fin à :
pn+1 = 3/4 − (13/4) × (1/5)n+1..
Pour cela, on peut partir de pn+1 = (1/5)pn + 3/5,
puis remplacer le pn par la donnée supposée
pn = 3/4 − (13/4) × (1/5)n.
On obtient donc
pn+1 = (1/5) × [ 3/4 − (13/4) × (1/5)n ] + 3/5
= (1/5) × (3/4) – (1/5) × (13/4) × (1/5)n + 3/5
= 3/20 – (13/5) × (1/5)n × (1/5)1 + 3/5
= 3/20 + 12/20 – (13/4) × (1/5)n+1
= 15/20 – (13/4) × (1/5)n+1
= 3/4 – (13/4) × (1/5)n+1
Donc la propriété est vraie au rang (n+1).
6) On a prouvé que pn = 3/4 − (13/4) × (1/5)n, calculons la limite.
Quand n tend vers +∞, lim (1/5)n = 0 car 0 < 1/5 < 1.
Par produit, quand n tend vers +∞, lim (13/4) × (1/5)n = 0.
Par différence, quand n tend vers +∞, lim pn = 3/4.
7) 3/4 − pn < 10-7
⇔ 3/4 − (3/4 – (13/4) × (1/5)n) < 10-7
⇔ 3/4 − 3/4 + (13/4) × (1/5)n < 10-7
⇔ (13/4) × (3/5)n < 10-7
⇔ (1/5)n < 10-7 × (4/13) en multipliant par 4/13 de chaque côté.
Maintenant on peut faire par tâtonnement (ou avec la calculatrice) mais la résolution classique avec le logarithme népérien est :
⇔ ln ((1/5)n) < ln [10-7 × (4/13)] car ln est strictement croissante sur l’intervalle des réels strictement positifs donc on conserve le sens des inégalités.
⇔ n × ln (1/5) < ln [10-7 × (4/13)]
car ln(an) = n × ln(a) d’après le cours.
⇔ n > ln [ 10-7 × (4/13) ] / ln(1/5) (on change de sens de l’inégalité car ln(1/5) est négatif à la calculette)
⇔ n > 10.7470 environ
⇔ n > 11 car n est entier naturel.
C’est à partir de n = 11 que l’écart entre pn et 3/4 devient plus petit que 10-7.
Bonne compréhension,
Sylvain Jeuland

