frenchmaths.com (par Sylvain Jeuland)

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) Montrer que M ∈ C ⇔ MI² = 25.

Ici, on a du ^→MA et du ^→MB, cela fait deux vecteurs différents et il serait mieux d’avoir un seul vecteur avec le point M.
Du coup, l’astuce habituelle est de prendre le point I le milieu de [AB]et de le mettre au milieu des vecteurs précités avec la relation de Chasles.

^→MA.^→MB = 16
⇔ (^→MI + ^→IA).(^→MI + ^→IB) = 16

L’idée est de développer avec la double distributivité qui marche avec les “.” comme les “×”.

⇔ ^→MI.^→MI + ^→MI.^→IB + ^→IA.^→MI + ^→IA.^→IB = 16

Quand on fait le produit scalaire de deux fois le même vecteur, cela donne la distance au carré, on enlève les flèches.

⇔ MI² + ^→MI.^→IB + ^→IA.^→MI + ^→IA.^→IB = 16

On peut inverser les vecteurs dans un produit scalaire pour avoir les ^→MI devant.

⇔ MI² + ^→MI.^→IB + ^→MI.^→IA + ^→IA.^→IB = 16

Là, il faut factoriser par ^→MI devant ^→IB et ^→IA.

⇔ MI² + ^→MI.(^→IB + ^→IA) + ^→IA.^→IB = 16

Comme I est le milieu de [AB], on a donc ^→IB + ^→IA = ^→0. On peut donc enlever le ^→MI.^→0 car cela donne 0.

⇔ MI² + ^→IA.^→IB = 16

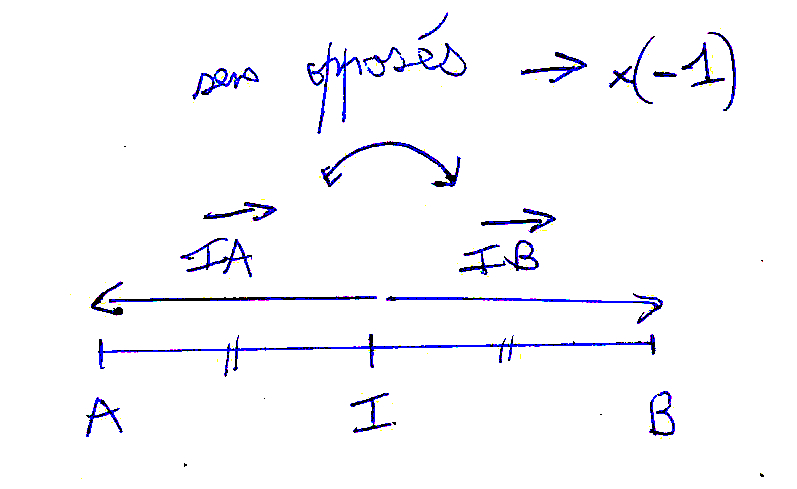
Les vecteurs ^→IA et ^→IB sont diamétralement opposés donc quand on fait le produit scalaire, cela donne IA × IB × (-1)
= AB/2 × AB/2 × (-1) (car IA et IB valent la moitié de AB).
= 6/2 × 6/2 × (-1)
= -9.

On obtient donc :

⇔ MI² – 9 = 16
⇔ MI² = 25

2) Déterminer alors précisément l’ensemble C :

On a donc MI = 5 car on est en géométrie donc on reste dans les nombre positifs.
Du coup, M est a distance de 5 du point I.

L’ensemble C des points vérifiant ^→MA.^→MB = 16 est le cercle de centre I milieu de [AB] et de rayon 5.

3) En utilisant les coordonnées des vecteurs, déterminer précisément l’ensemble D des points M du plan tels que ^→AM.^→BC = 3 :

A(-1 ; 2), B(2 ; -2), C(-2 ; -1) d’après l’énoncé.

On va utiliser la formule du cours avec les coordonnées :

xx’ + yy’

Pour les coordonnées du vecteur ^→BC,
on fait x’ = x_C – x_B = -2 – 2 = -4
et y’ = y_C – y_B = -1 – (-2) = 1

Pour les coordonnées du vecteur ^→AM,
on fait x = x_M – x_A = x_M – (-1) = x_M + 1
et y = y_M – y_A = y_M – 2.

On obtient donc xx’ + yy’ = 3
⇔ (x_M + 1)×(-4) + (y_M – 2)*1 = 3
⇔ -4x_M – 4 + y_M – 2 = 3
⇔ -4x_M + y_M – 6 – 3 = 0

L’ensemble D des points M est la droite d’équation cartésienne
-4x + y – 9 = 0 avec x et y les coordonnées des points de la droite.

Bonne compréhension,
Sylvain