Exercice : Clic droit vers l’exercice
Tout le corrigé :
1) Pour avoir le coût marginal Cm(x), on fait la fonction dérivée du coût total
CT(x) = 2x2 + xe-2x + 3.
CT(x) = 2x2 + u(x) × v(x)
avec u(x) = x,
donc u ‘ (x) = 1,
avec v(x) = e-2x + 3,
donc v ‘ (x) = -2 × e-2x + 3 avec la dérivée de l’exponentielle :
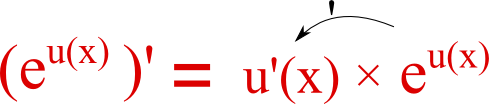
Donc C ‘ T(x) = 2 × 2x + (u ‘ (x) × v(x) + u(x) × v ‘ (x))
= 4x + 1 × e-2x + 3 + x × (-2 × e-2x + 3)
On obtient en factorisant par l’exponentielle :
Cm(x) = 4x + (1 – 2x) × e-2x + 3
2) Pour calculer le coût marginal pour 150 articles, on fait :
Cm(1.5) = 4 × 1.5 + (1 – 2 × 1.5) × e-2 × 1.5 + 3
= 6 – 2 × e-2 × 1.5 + 3
= 6 – 2 × e0
= 6 – 2 × 1
= 4 milliers d’euros.
CM(x) = CT(x)/x
3) Expression de CM(x) :
CM(x) = (2x2 + xe-2x + 3)/x
= (x × [2x + e-2x + 3])/x
(en factorisant par x au numérateur)
= 2x + e-2x + 3
(en simplifiant x/x = 1).
4) Déterminer CM ‘ (x) :
CM(x) = 2x + e-2x + 3
On utilise à nouveau la formule de la dérivée de l’exponentielle vue au-dessus.
CM ‘ (x) = 2 + (-2) × e-2x + 3
= 2 – 2e-2x + 3
= 2 × (1 – e-2x + 3)
(comme je vois 2 et 2 dans chaque terme, je factorise par 2)
5) Résolvons l’équation 1 – e-2x + 3 = 0 :
1 – e-2x + 3 = 0
⇔ 1 = e-2x + 3
⇔ e0 = e-2x + 3
⇔ 0 = -2x + 3
⇔ 2x = 3
⇔ x = 3/2
S = {3/2}
6) Résolvons l’équation 1 – e-2x + 3 > 0 :
1 – e-2x + 3 > 0 (expression positive)
⇔ 1 > e-2x + 3
⇔ e0 > e-2x + 3
⇔ 0 > -2x + 3
(car exp est strictement croissante, on ne change pas le sens de l’inégalité)
⇔ 2x > 3
⇔ x > 3/2
(x à droite de 3/2)
S = ]3/2 ; +∞[
7) Pour obtenir les variations de CM, il nous faut le signe de CM ‘ (x) qui est un produit. On fait le tableau suivant :
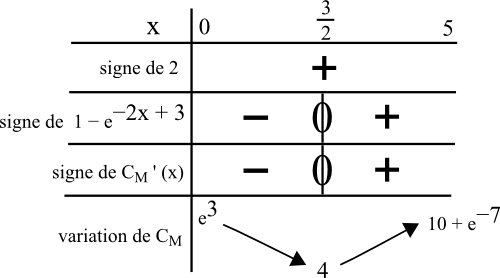
8) D’après le tableau de variation de CM, on voit que le coût moyen est minimal pour une quantité de 1.5 centaine d’articles.
Donc CM(1.5) = 2 × 1.5 + e-2 × 1.5 + 3
= 3 + e0
= 3 + 1 = 4.
Le coût moyen minimal est de 4 milliers d’euros.
R(x) = 7x,
B(x) = R(x) − CT(x).
Par lecture graphique déterminer :
9) Le coût marginal est décroissant, soit Cm décroissante. Or Cm est la dérivée de CT donc cela équivaut à C ‘ T décroissante.
Or C ‘ T décroissante
⇔ C ‘ ‘ T(x) négatif
⇔ CT concave
⇔ C’est quand les tangentes à la courbe sont au-dessus de cette même courbe, c’est-à-dire avant le point d’inflexion de la courbe qui est proche du point d’abscisse 0.7.
L’intervalle de rendement marginal croissant est de [0 ; 0.7].
10) Le coût moyen minimal est atteint en x = 1.5, donc on regarde le coût total qui vaut 6.
Pour obtenir ce coût moyen, on peut rediviser ce coût total par la quantité.
6/1.5 = 4.
On retrouve le coût moyen calculé plus haut.
11) Le bénéfice est positif quand la recette est supérieure au coût. Il faut déterminer les abscisses des points des courbes quand la droite des recettes est au-dessus de la droite du coût.
On remarque que le bénéfice est positif pour des quantités allant de 0.6 à 3.5 centaines d’articles.
12) Pour obtenir la quantité x0 avec le bénéfice maximal, il faut regarder à quel endroit l’écart entre la droite de la recette et la courbe du coût est le plus grand. D’après le graphique, x0 = 2.2 centaines d’articles environ.
13) Avec la calculatrice, déterminons l’intervalle (à un article près) pour avoir un bénéfice positif. Pour cela, on a besoin de la formule du bénéfice B(x) qui est égale à
R(x) – CT(x)
= 7x – (2x2 + xe-2x + 3)
Je rentre cette formule dans le tableur de la calculatrice.
D’abord de 0 à 1, ensuite de 3 à 4 car nous avions vu dans une question précédente que les bornes étaient environ de 0.6 et de 3.5.
Je commence par mettre le pas (step) à 0.1, la fonction B(x) change de signe entre 0.6 et 0.7, puis entre 3.4 et 3.5.
Puis j’affine le pas au centième pour arriver à l’article près (x étant en centaines d’articles). On a :
B(0.62) = -0.0325 (au dix-millième près)
B(0.63) = 0.0269 (au dix-millième près)
B(3.49) = 0.0046 (au dix-millième près)
B(3.50) = -0.0064 (au dix-millième près)
On conserve les valeurs où les images sont positives.
Donc l’entreprise fait un bénéfice positif
sur l’intervalle [0.63 ; 3.49].
Bonne compréhension,
Sylvain Jeuland

