Exercice : Clic droit vers l’exercice
Tout le corrigé :
0) Démontrer que la fonction h : x → x2 + 4 est croissante sur [0 ; +∞ [ :
Pour démontrer qu’une fonction est croissante en seconde, la propriété du cours dit qu’il faut :
* Partir de a < b. C’est à dire écrire “a < b” sur la feuille.
* Puis arriver à f(a) ≤ f(b).
En effet, si “a < b donne f(a) ≤ f(b)“, cela veut dire que la fonction f est croissante comme c’est illustré sur l’image ci-dessous.
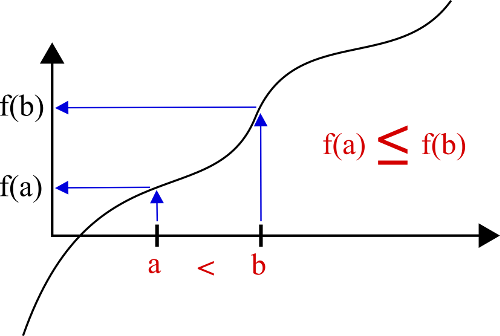
On voit bien que si on prend a < b et qu’on arrive à f(a) ≤ f(b), alors la courbe monte entre les deux points. Attention, il faut dire “pour tout a et b tels que a < b“.
Ici, on veut sur [0 ; +∞ [, c’est important avec la fonction carré car la variation change si on est dans les négatifs ou si on est dans les positifs.
Soit n’importent quels a et b tels que 0 ≤ a < b.
En passant au carré, cela donne : 02 ≤ a2 < b2 car la fonction carré est strictement croissante sur [0 ; +∞ [ (donc on ne change pas le sens des inégalités).
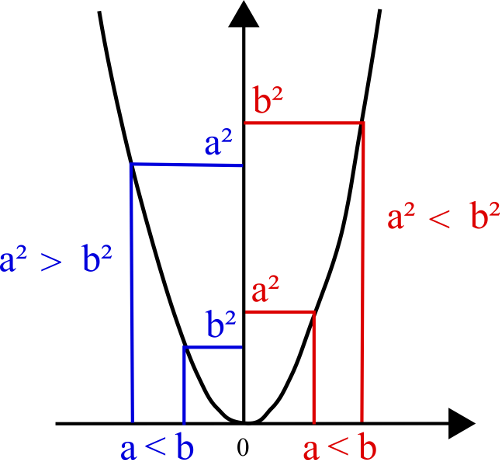
On voit bien à droite dans les positifs que l’on garde le sens “plus petit ou égal”.
Rédaction :
Sur [0 ; +∞ [ : 0 ≤ a < b
⇔ 02 ≤ a2 < b2 (car “carré” est strictement croissante sur R+)
⇔ 02 + 4 ≤ a2 + 4 < b2 + 4 (on additionne)
⇔ f(0) ≤ f(a) < f(b)
On a donc “a < b donne f(a) < f(b)” ou même “a < b donne f(a) ≤ f(b)” avec une inégalité large. Donc la fonction f croissante sur [0 ; +∞ [.
1) Représenter dans un même repère les courbes Cf et Cg des fonctions f et g sur l’intervalle [-4 ; 6] :
Rédaction :
On fait un tableau (tableur ou calculatrice) avec les valeurs de x allant de -4 à 6 (de 1 en 1 par exemple). On met les f(x) en dessous des x et les g(x) encore en dessous. Puis on place les points (x ; f(x)) et (x ; g(x)) sur le repère et on les relie en courbe (ou en droite avec g(x)). Cela donne :
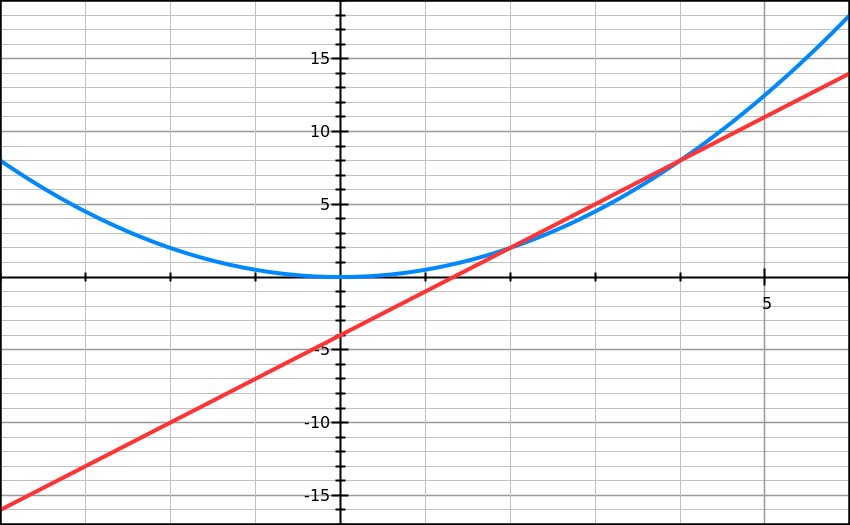
La parabole bleue est Cf et la droite rouge est Cg. Écris bien Cf et Cg sur le graphique.
2) Résoudre graphiquement l’équation f(x) = g(x) :
Rédaction :
Pour résoudre graphique f(x) = g(x), on regarde les points d’intersection de Cf et Cg et on note les abscisses comme solutions.
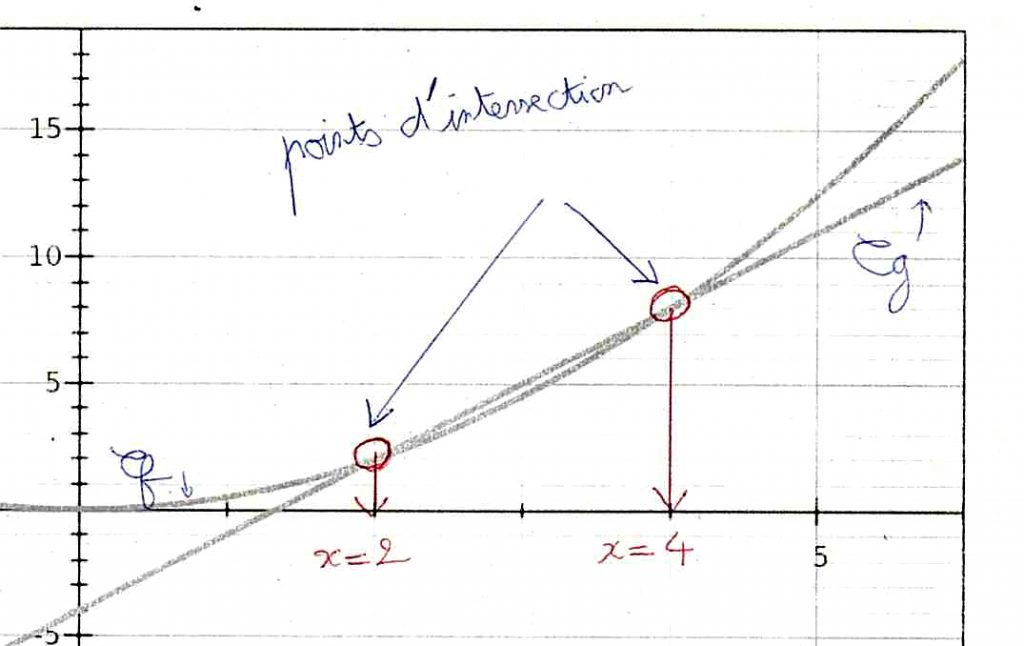
On obtient 2 et 4 comme abscisses des points d’intersection de Cf et Cg. Donc S = {2 ; 4} graphiquement.
3) Montrer que pour tout réel x, (1/2) x2 – 3x + 4 = (1/2) (x – 2)(x – 4) :
Rédaction :
Pour montrer une égalité de ce type, on part de la forme factorisée (celle avec le produit et les parenthèses) vers la forme développée.
(1/2) (x – 2)(x – 4)
= 0.5(x – 2)(x – 4)
= (0.5x – 1)(x – 4), en distribuant le 0.5 sur le (x – 2), 0.5×2 = 1.
= 0.5x × x – 0.5x × 4 – 1 × x – 1 × (-4).
= 0.5x2 – 2x – 1x + 4
= 0.5x2 – 3x + 4.
= (1/2) x2 – 3x + 4.
4) En déduire la résolution algébrique (par le calcul) de l’équation f(x) = g(x) :
Rédaction :
On passe tout à gauche en soustrayant les deux membres de l’égalité par g(x) :
f(x) = g(x)
⇔ f(x) – g(x) = 0
⇔ 0.5x2 – (3x – 4) = 0
⇔ 0.5x2 – 3x + 4 = 0
⇔ 0.5(x – 2)(x – 4) = 0 (d’après le 3)).
⇔ 0.5=0 ou x-2=0 ou x-4=0 car un produit de facteurs est nul si au moins l’un des facteurs est nul.
0.5=0 est impossible, x = 2 ou x = 4.
Donc les solutions de l’équation f(x) = g(x) sont 2 et 4.
5) A l’aide des courbes représentatives des fonctions f et g, résoudre l’inéquation
f(x) ≤ g(x) :
Rédaction :
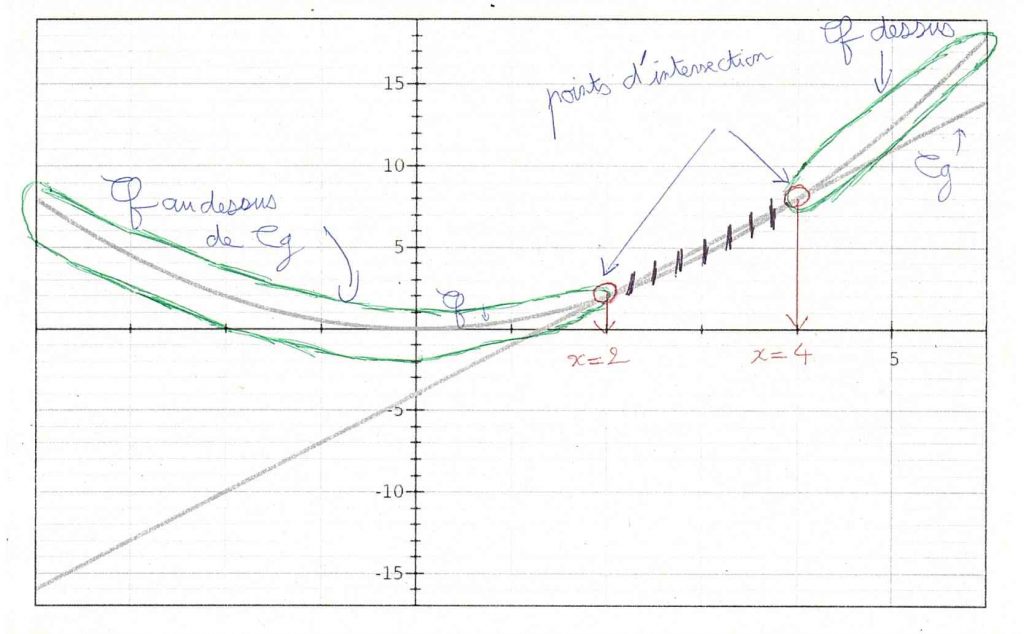
J’ai entouré en vert les morceaux de courbes où Cf est au dessus de Cg :
Sur [-6 ; 2] et [4 ; 6], f(x) ≥ g(x).
J’ai hachuré en noir les morceaux de courbes où Cf est en dessous de Cg :
Sur [2 ; 4], f(x) ≤ g(x). C’est ce qu’on veut.
Donc S = [2 ; 4].
D’ailleurs j’aurais mieux fait d’entourer en vert quand Cf est en dessous de Cg pour que ça colle bien à la question 5).
Bonne compréhension,
Sylvain Jeuland


