Exercice : Clic droit vers l’exercice
Tout le corrigé :
→SI = (1/3)→SA
→SJ = (1/3)→SD
1) Je découpe le segment [SA] en trois et je place I à 1/3 du segment en partant de S vers A.
Je découpe le segment [SD] en trois et je place J à 1/3 du segment en partant de S vers D.
(AI) et (DJ) sont sécantes en S. A, I, S et D, J, S sont alignés dans le même ordre. Les rapports SI/SA et SJ/SD sont égaux (1/3).
D’après la réciproque du théorème de Thalès, (IJ) et (AD) sont parallèles.
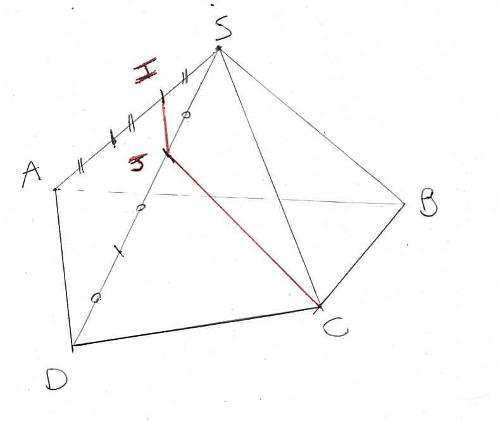
(ABCD) et (CIJ) sont deux plans sécants qui contiennent respectivement (AD) et (IJ) qui sont deux droites parallèles.
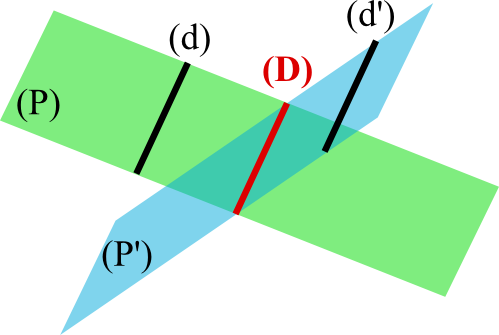
Voici le Théorème du toit : Si on a deux droites parallèles d1 et d2, un plan P1 contenant d1, un plan P2 contenant d2 et P1 et P2 sécants, alors l’intersection d des deux plans est une droite parallèle aux droites d1 et d2.
Donc l’intersection de (ABCD) et (CIJ) est une droite parallèle à (IJ) et (AD).
Or le point C appartient à la fois aux deux plans, il est donc sur la droite d’intersection qu’on peut tracer à partir de C en suivant une parallèle à (IJ) et (AD).
Cette droite est sur la base (ABCD), elle atteint le segment [AB].
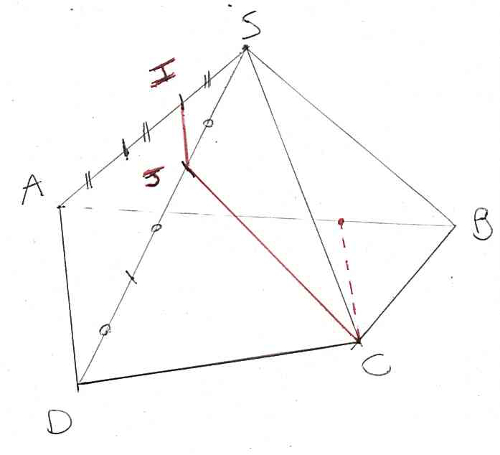
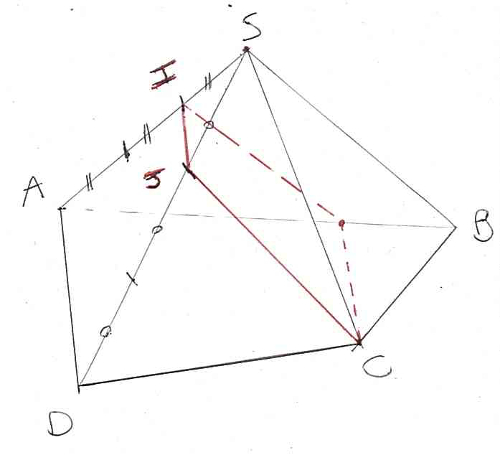
2) Pour tracer cette section, on relie les points qui sont à la fois sur (CIJ) et sur la pyramide : il s’agit de I, J et C. On a tracé le segment de la face du dessous grâce au théorème du toit dans le 1).
On obtient donc un second point de (CIJ) sur la face arrière (SAB) en plus du point I. On relie ces deux points pour obtenir la droite d’intersection de (CIJ) et (SAB).
Autre pyramide SABCD telle que (AB) et (CD) se coupent en E.
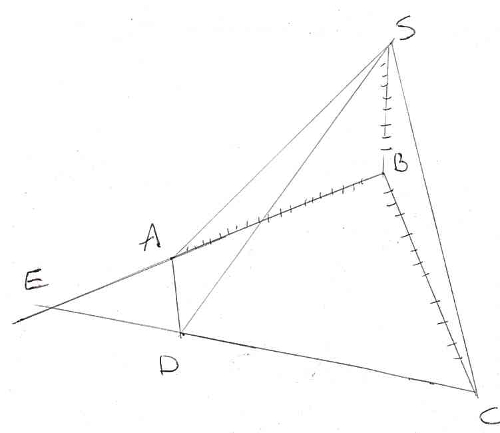
3) L’intersection de deux plans sécants est une droite.
Je vais trouver deux points qui sont à la fois sur les plans (SAB) et (SDC).
Le point S est cité deux fois, donc il appartient à l’intersection des deux plans (SAB) et (SDC).
Par construction, E est à la fois sur la droite (AB) et la droite (DC). Il appartient donc à la fois au plan (SAB) et au plan (SDC).
Comme S et E appartiennent à l’intersection des deux plans, alors la droite (SE) est l’intersection des deux plans (SAB) et (SDC).
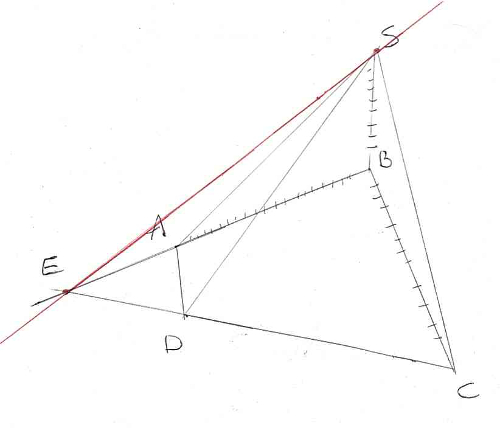
Un plan P parallèle à (ES) coupe (SA) en I, (SB) en J, (SC) en K, (SD) en L.
4) Là encore on utilise le théorème du toit dans une formulation un peu différente avec comme premier plan (SAB) et comme second plan P qui est parallèle à (ES).
Théorème du toit version 2 : Si une droite (d’) est parallèle à deux plans sécants P1 et P2 , alors elle est parallèle à leur droite d’intersection (d).
On sait que (ES) est parallèle à P d’après l’énoncé, et (ES) est parallèle à (SAB) car elle est incluse dedans. Donc (ES) est parallèle à la droite d’intersection de P et de (SAB) qui est la droite (IJ) car P coupe (SA) en I et (SB) en J.
De la même manière avec (SDC) et (ES), on prouve que (ES) est parallèle à (KL), K et L étant les points d’intersection de P et de (SDC).
Or deux droites parallèles à une même troisième sont parallèles entre elles, donc (IJ) et (KL) sont parallèles.
Bonne compréhension,
Sylvain Jeuland

