Exercice : Clic droit vers l’exercice
Tout le corrigé :
1) Pour calculer la mesure d’un principale d’un angle, l’idéal est de mettre 2π sous la forme d’une fraction avec le même dénominateur que notre angle.
2π = 8π/4
La mesure principale doit se situer dans l’intervalle ]-π ; π]. Là aussi, l’idéal est de mette les π sous la forme d’une fraction avec le même dénominateur que notre angle.
]-π ; π] = ]-4π/4 ; 4π/4].
Si l’angle de départ est au delà de l’intervalle ]-π ; π], il faut enlever les 2π jusqu’à l’atteindre.
Si l’angle de départ est en deçà de l’intervalle ]-π ; π], il faut ajouter les 2π jusqu’à l’atteindre.
Du coup, comme j’ai tout mis sur le même dénominateur et qu’il y a des π partout, on peut partir de -35 (pour -35Π/4), ajouter plusieurs fois 8 (pour 8π/4) pour arriver dans l’intervalle ]-4 ; 4] (pour ]–4π/4 ; 4π/4]).
-35 + 8 = -27
-27 + 8 = -19
-19 + 8 = -19
-11 + 8 = -3
-3 appartient à ]-4 ; 4] donc la mesure principale est -3Π/4.
2) Pour résoudre sur [0 ; 2π] une équation du type
sin(x) = -√2/2,
il faut déjà arriver à la forme :
sin a = sin b.
Pour cela, regardons à quel angle correspond -√2/2 sur le cercle trigonométrique. Comme on parle de sinus, on s’occupe de la hauteur -√2/2.
Tout d’abord, -√2/2 correspond à environ -0,71 pour un cercle trigo qui a pour rayon 1.
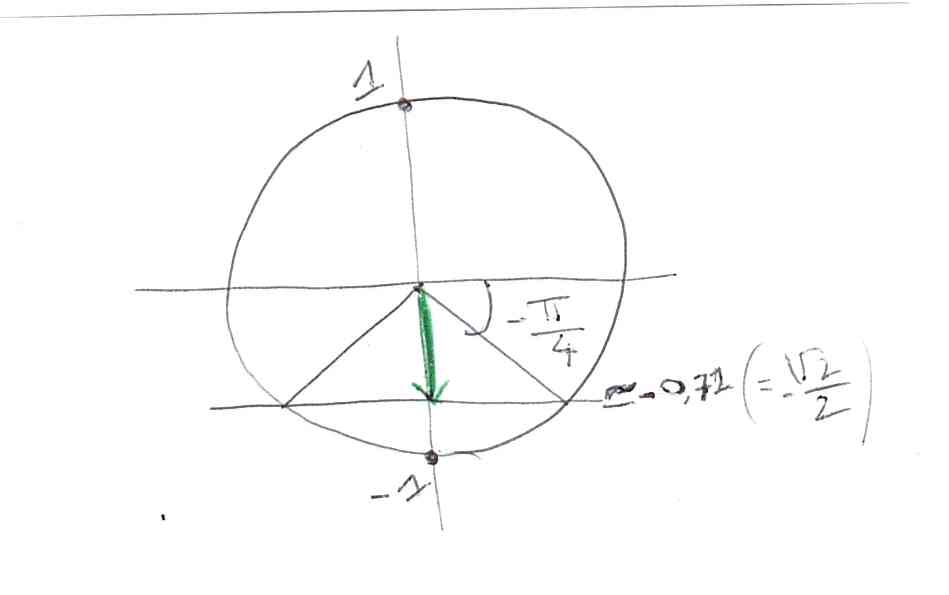
Comme +√2/2 est le sinus de π/4,
la hauteur -√2/2 correspond à –π/4.
On obtient donc : sin x = sin (–π/4).
D’après le cours, si sin a = sin b, cela veut dire que :
a = b + 2π*k (k ∈ Z),
ou
a = π – b + 2π*k (k ∈ Z).
Dans notre cas :
x = –π/4 + 2π*k (k ∈ Z),
ou
x = π – (-π/4) + 2π*k (k ∈ Z).
⇔
x = –π/4 + 2π*k (k ∈ Z),
ou
x = 5π/4 + 2π*k (k ∈ Z).
Ces deux égalités sont les solutions sur R, maintenant il nous les faut sur l’intervalle [0 ; 2π]. Pour cela, on prend la première des égalités et on parcourt les différentes de k. 0, -1, -2, etc, puis 1, 2, etc. On vérifie si les valeurs trouvées sont dans l’intervalle ou non.
Pour la première égalité :
k = 0 donne –π/4 qui n’est pas dans l’intervalle car en dessous. On ne descendra pas dans les k négatifs. Non.
k = 1 donne –π/4 + 2π soit 7π/4. Celui-ci est bien dans l’intervalle [0 ; 2π] voulu car 8/4 = 2. OK.
k = 2 donne 15π/4, donc on dépasse l’intervalle par le dessus. Non et on s’arrête là.
Pour la seconde égalité :
k = 0 donne 5π/4, on est bien dedans. OK.
k = -1 donne -3π/4, on est en dessous. Non.
k = 1 donne 13π/4, on est au dessus. Non et on s’arrête là.
Pour conclure, S = { 7π/4 ; 5π/4 }.
3-4-5-6) On a (→u, →v) = π/3
et (->u, ->w) = π/4.
3) (→u, –→v) :
Lorsqu’on a “un seul moins” devant un vecteur, cela renverse ce vecteur vers l’autre sens donc il se crée un demi-tour, soit un changement d’angle de π.
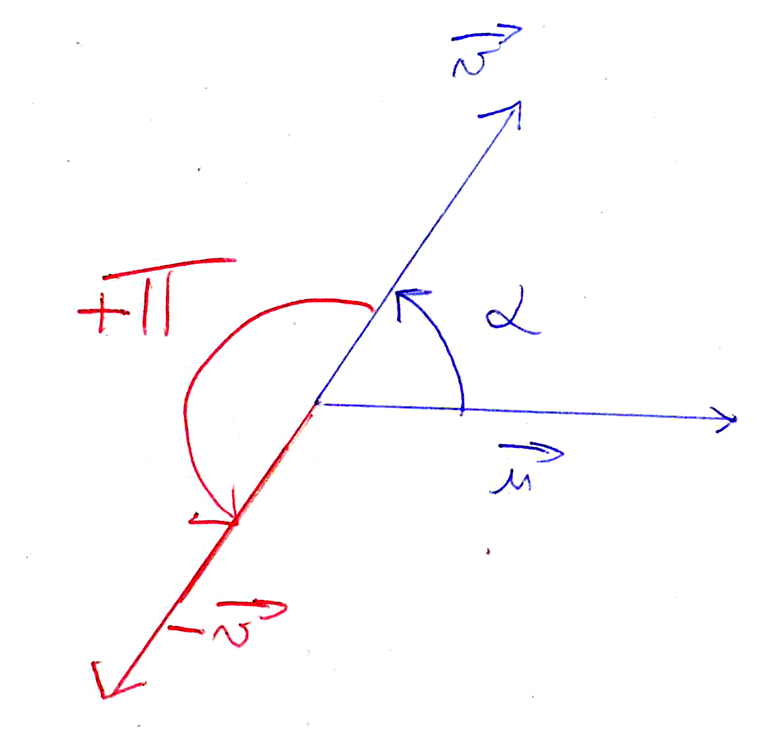
On a donc : (→u, –→v) = (→u, →v) + π
= π/3 + π
= 4π/3
= -π/3 (mesure principale).
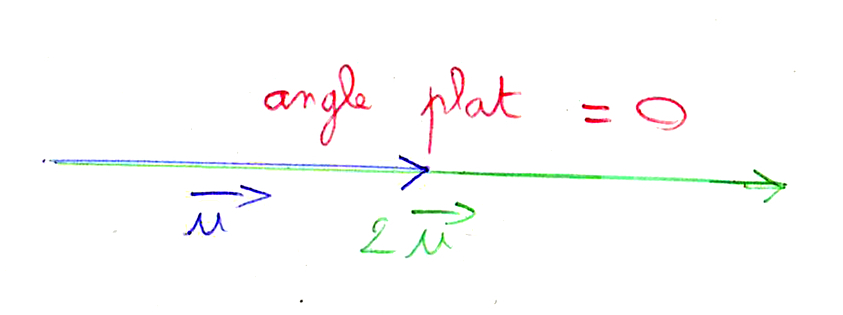
4) (→u, 2→u) :
On a les vecteurs →u et →u qui sont dans la même direction et le même sens. Donc l’angle est nul. Comme 2 est positif, cela ne change rien au sens de ->u.
Donc (→u, 2→u) = 0.
5) (→v, →w) :
Comme on connaît →u et →v donc on peut faire Chasles entre →v et →w en plaçant →u au milieu.
(→v, →w) = (→v, →u) + (→u, →w).
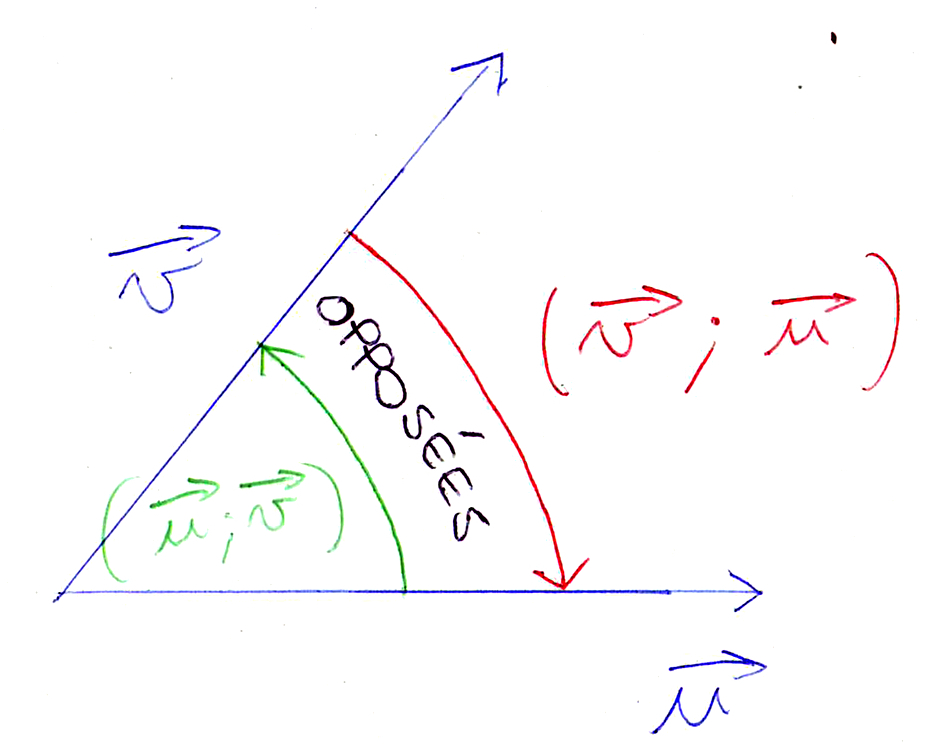
(→v, →u) se calcule en inversant le sens de
(→u, →v) car si on va de →v vers →u, c’est en sens contraire de →u vers →v.
Donc :
(→v, →u) = -(→u, →v).
(→v, →w) = (→v, →u) + (→u, →w)
= -(→u, →v) + (→u, →w)
= –π/3 + π/4
= –4π/12 + 3π/12
= –π/12
6) (-2→w, -5→u) :
Ici, on a deux “moins”. Comme vu dans le petit a), on peut enlever celui du vecteur gauche en ajoutant π à l’angle.
(-2→w, -5→u) = (2→w, -5→u) + π
On peut enlever celui du vecteur droit en ajoutant encore π à l’angle.
(2→w, 5→u) + π = (2→w, 5→u) + π + π
Les coefficients positifs ne changent pas la valeur de l’angle.
(2→w, -5→u) + π + π = (→w, →u) + 2π
L’ajout de 2π représente un tour complet de l’angle donc on peut enlever le 2π car cela ne change rien à sa valeur.
(→w, →u) + 2π = (→w, →u)
Comme vu précédemment, on peut échanger les vecteurs en prenant l’opposé car on change de sens donc :
(→w, →u)
= -(→u, →w)
= –π/4
Du coup, (-2→w, -5→u) = –π/4.
Bonne compréhension,
Sylvain Jeuland

