frenchmaths.com (par Sylvain Jeuland)

Exercice : Clic droit vers l’exercice

Tout le corrigé :

1) Pour démontrer que ABDC est un parallélogramme, il suffit de démontrer que ^→AB = ^→CD.
Les deux dernières lettres sont inversées !

^→AB
{
x_^→AB = x_B – x_A = 3 – (-2) = 5 ;
y_^→AB = y_B – y_A = 3 – 4 = -1.

^→CD
{
x_^→CD = x_D – x_C = 4 – (-1) = 5 ;
y_^→CD = y_D – y_C = -1 – 0 = -1.

Les coordonnées des vecteurs AB et CD sont les mêmes donc ^→AB = ^→CD.
Donc ABDC est un parallélogramme.

2) Si un parallélogramme a deux côtés consécutifs de même longueur, alors c’est un losange.
Calculons donc AB et BD séparément (qui sont deux côtés consécutifs dans le parallélogramme).
Pour ça, on utilise la formule de la distance :

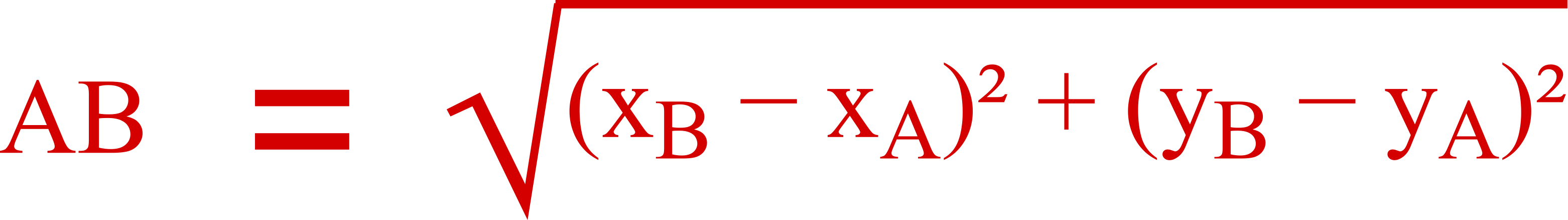
On a déjà calculé x_B – x_A et y_B – y_A au dessus :

AB = √( 5² + (-1)² )
= √26.

BD = √( (x_D – x_B)² + (y_D – y_B)² )
= √( (4 – 3)² + ((-1) – 3)² )
= √( 1² + (-4)² )
= √17.

AB différent de BD donc les côtés consécutifs ne sont pas égaux, donc ABDC n’est pas un losange.

3) On veut que GHKL soit un parallélogramme donc ^→GH doit être égal à ^→LK.
Cette égalité vectorielle équivaut à un système de coordonnées de vecteurs.

{
x_^→GH = x_^→LK,
y_^→GH = y_^→LK
⇔
{
x_H – x_G = x_K – x_L (d’après le cours),
y_H – y_G = y_K – y_L
⇔
{
2 – 0 = -2 – x_L,
1 – 0 = 3 – x_L
⇔
{
2 + 2 = – x_L
1 – 3 = – y_L
(en isolant les coordonnées de L à droite)
⇔
{
x_L = -4
y_L = 2
(en multipliant par -1)

4) Pour démontrer que ^→GE = ^→FK, on calcule les coordonnées de ces vecteurs séparément.

x_^→GE = x_E – x_G = -3 – 0 = -3
y_^→GE = y_E – y_G = -2 – 0 = -2
x_^→FK = x_K – x_F = -2 – 1 = -3
y_^→FK = y_K – y_F = 3 – 5 = -2

On obtient
x_^→GE = x_^→FK,
y_^→GE = y_^→FK.

Les deux vecteurs ont même coordonnées donc ils sont égaux.
Du coup, GEKF est un parallélogramme.

5) Pour montrer que [FE] et [HL] ont même milieu, utilisons la formule des coordonnées d’un milieu sur les deux segments.

Milieu de [FE] :
^{(x_F + x_E)}/₂ = ^{(1 + (-3))}/₂ = ^(-2)/₂ = -1,
^{(y_F + y_E)}/₂ = ^{(5 + (-2))}/₂ = ³/₂.

Milieu de [HL] :
^{(x_H + x_L)}/₂ = ^{(2 + (-4))}/₂ = ^(-2)/₂ = -1,
^{(y_H + yL)}/₂ = ^{(1 + 2)}/₂ = ³/₂.

Les deux milieux ont les mêmes coordonnées, donc c’est le même milieu pour les deux segments.

Bonne compréhension,
Sylvain Jeuland