Maths de première : exercice sur dérivée, fonction, tangente, nombre dérivé, courbe, trinôme, racine, rationnelle, quotient, produit.
Exercice N°568 :

Exercice N°568 :
On considère la fonction f définie par :
f(x) = 1/(1 – x)
pour tout x ≠ 1.
1) A l’aide du taux d’accroissement, étudier la dérivabilité de la fonction f en a = 3. Si possible, donner le nombre dérivé.
On considère la fonction g définie sur [1 ; +∞[ par :
g(x) = √(x – 1).
2) Cette fonction g est-elle dérivable en a = 5 ? On répondra à l’aide du taux d’accroissement et, s’il existe, on donnera le nombre dérivée.
On considère la fonction h définie par :
h(x) = 3x2 + 5x – 2
pour tout x de R.
3) Déterminer une équation de la tangente à la courbe représentative de h au point d’abscisse (-3).
On a représenté la courbe d’une fonction k et certaines de ses tangentes.
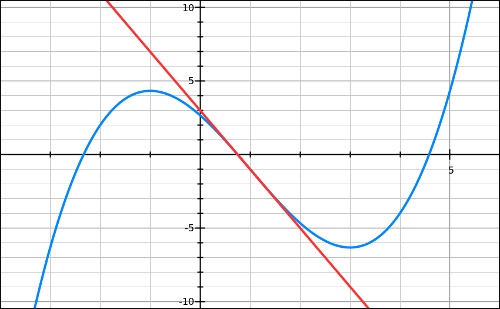
4) Lire k ‘ (-1) et k ‘ (1).
567) Pour chaque fonction, justifier qu’elle est dérivable et donner sa fonction dérivée sur l’intervalle I.
5) p(x) = (x – 1)√x sur ]2 ; +∞[,
6) q(x) = 1/(2x2 – 8) sur ]-2 ; 2[,
7) r(x) = (2x – 5)/(x2 + 6) sur R.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, dérivée, fonction, tangente.
Exercice précédent : Probabilités – Arbre, tirage sans remise, indiscernable – Seconde

