Maths de première sur la dérivation : exercice de dérivée de polynôme avec coût, recette, bénéfice, calculs, recette,variation, maximum.
Exercice N°290 :
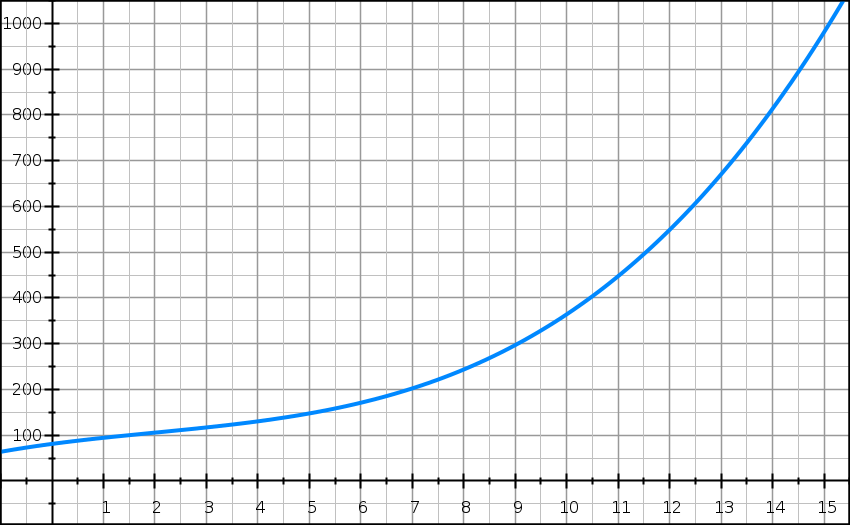
Soit C la fonction définie pour tout réel x élément de l’intervalle ]0 ; 15] par :
C(x) = x3/3 − 2x² + 15x + 81.
La fonction C modélise le coût total de production, exprimé en milliers d’euros, de x milliers d’articles fabriqués. La courbe CT représentative de la fonction C est tracée ci-dessus dans un repère orthogonal.
On suppose que chaque article produit est vendu au prix de 60 €.
On note R(x) la recette, exprimée en milliers d’euros, générée par la production et la vente de x milliers d’articles.
1) Dans le repère précédent, tracer la courbe représentative de la fonction recette.
2) Déterminer graphiquement les valeurs arrondies au millier près des bornes de l’intervalle dans lequel doit se situer la production pour que l’entreprise réalise un bénéfice positif.
Le bénéfice est la fonction B définie sur l’intervalle ]0 ; 15]
par B(x) = R(x) − C(x).
3) Calculer B ‘ (x).
4) Étudier les variations de la fonction B.
5) En déduire la production x0 pour laquelle le bénéfice est maximal.
Quel est le montant en euro de ce bénéfice maximal ?
La fonction coût moyen, notée CM, est la fonction définie sur l’intervalle
]0 ; 15] par
CM(x) = C(x)/x.
6) Sur le graphique précédent, placer le point A sur la courbe CT tel que la droite (OA) soit tangente à CT.
On appelle a l’abscisse du point A.
7) Montrer que le coefficient directeur de la droite (OA) est égal à CM(a).
8) Par lecture graphique, conjecturer les variations de la fonction CM sur l’intervalle ]0 ; 15].
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, dérivée, polynôme, coût.
Exercice précédent : Dérivation – Fonction rationnelle, variation, tangente – Première


Bonjour, je ne comprends pas dès la première question…
La recette est le prix de vente fois le nombre d’unités vendues.
Cela fait donc : R(x) = 60x. C’est une fonction affine dont la droite passe par l’origine avec 60 comme coefficient directeur.