Maths de première sur un exercice avec algorithme et suite géométrique. Problème, formules récurrente et explicite, raison, premier terme.
Exercice N°610 :

Exercice N°610 :
2100 m3 d’eau sont répartis entre deux bassins A et B avec respectivement 700 m3 et 1400 m3.
Chaque jour, 10 % du volume d’eau présent dans le bassin B au début de la journée est transféré vers le bassin A.
Et, chaque jour, 5 % du volume présent du bassin A au début de la journée est transféré vers le bassin B.
Pour tout entier naturel n > 0, on note an (respectivement bn) le volume d’eau, en m3, dans le bassin A (respectivement B) à la fin du n-ième jour.
1) Quelles sont les valeurs de a1 et de b1 ?
2) Quelle est la valeur de an+bn pour tout entier naturel n > 0 ?
3) Justifier que, pour tout entier naturel n > 0,
an+1 = 0.85an + 210.
L’algorithme ci-contre permet de déterminer la plus valeur de n à partir de laquelle an ≥ 1350.
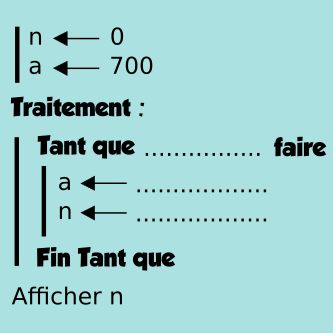
4) Compléter cet algorithme.
Pour tout entier n > 0, on note
un = an – 1400.
5) Montrer que la suite (un) est géométrique. Préciser sa raison et son premier terme u1.
6) Exprimer un en fonction de n.
7) En déduire an en fonction de n.
8) En déduire au bout de combien de jours le bassin A contient plus de 1350 m3.
Bon courage,
Sylvain Jeuland
Mots-clés de l’exercice : exercice, algorithme, suite géométrique.
Exercice précédent : Dérivations – Nombres dérivés, polynôme, rationnelle, racine – Première

