Maths sur les suites : exercice de récurrence avec somme en terminale. Limite, conjecture, calculs de termes, raisonnement.
Exercice N°180 :
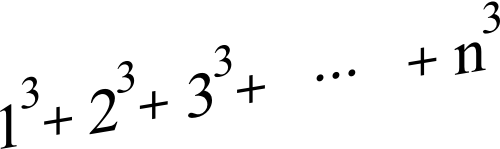
On considère la suite (un) définie pour tout entier n ∈ N∗ par :
u1 = 1,
un+1 = un + (n + 1)3.
1) Calculer les quatre premiers termes de la suite (un).
2) Démontrer par récurrence que, pour tout entiern ∈ N∗,
un = 13 + 23 + · · · + n3.
3) En déduire que, pour tout entier non nul,
un ≥ n3.
4) Calculer la limite de un.
Pour tout entier n ∈ N∗, on note :
Sn = 1 + 2 + · · · + n.
5) Rappeler l’expression de Sn en fonction de n.
6) Calculer S1, S2, S3 puis S4.
7) Émettre une conjecture sur un et Sn.
8) Prouver cette conjecture par récurrence.
Bon courage,
Sylvain Jeuland
Pour avoir le corrigé (57 centimes d’euros),
clique ici sur le bouton ci-dessous :
Pour avoir tous les corrigés actuels de ce chapitre (De 77 centimes à 1.97 euros selon le nombre d’exercices),
clique ici sur le bouton ci-dessous :
77 centimes pour 2 exercices – 97 cts pour 3 – 1.17€ pour 4 – 1.37€ pour 5 – 1.57€ pour 6 – 1.67€ pour 7 – 1.77€ pour 8 – 1.87€ pour 9 et 1.97€ pour 10 et +.
Mots-clés de l’exercice : exercice, récurrence, somme, terminale.
Exercice précédent : Probabilités – Conditionnelles, binomiale, espérance – Terminale

