Exercice : Clic droit vers l’exercice
Tout le corrigé :
1) Pour donner l’expression du bénéfice, il faut écrire
B(x)= R(x) – C(x)
avec R(x) = prix_unitaire×quantité = 100 × x = 100x.
Donc B(x) = 100x – (x² + 50x + 100)
= 100x – (x² + 50x + 100)
= -x² + 50x – 100.
Donc le bénéfice horaire réalisé par la fabrication et la vente de x appareils est B(x) = -x² + 50x – 100 pour x appartenant à [5 ; 100].
2) Calcul de la dérivée :
On a B(x) = -x² + 50x – 100.
La dérivée de -x² est -2x.
La dérivée de 50x est le coefficient devant le x soit 50.
Le coefficient d’une constante (ici -100) est 0.
Donc B ‘ (x) = -2x + 50.
Étudions le signe B ‘ (x) pour obtenir les variations de B :
Pour déterminer le signe de B ‘ (x), ma méthode est de résoudre une inéquation avec ≥ 0 car nous sommes dans le cas d’une fonction affine (cela fonctionne aussi avec les fonctions exponentielles et logarithmes népérériens). Cela permet de déterminer si on met le + à gauche ou à droite de la valeur annulante.
B ‘ (x) ≥ 0 (on cherche donc où mettre le + dans le tableau de signes)
⇔ -2x + 50 ≥ 0
⇔ -2x ≥ -50
⇔ x ≤ 25 (comme on divise par un négatif, on change le sens de l’inégalité)
Les x ≤ 25, cela correspond aux “x” sont à gauche de 25.
Donc, on mettra le + quand “x” sera à gauche de 25.
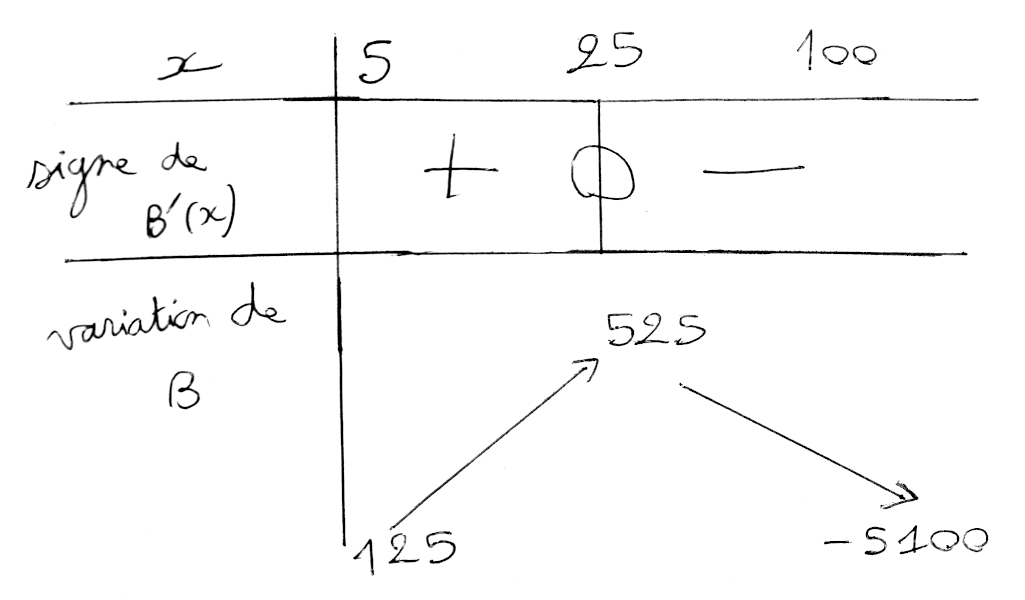
B(5) = -5² + 50×5 – 100
= -25 + 250 – 100
= 225 – 100
= 125.
B(25) = -25² + 50×25 – 100
= -625 + 1250 – 100
= 625 – 100
= 525.
B(100) = -100² + 50×100 – 100
= -10000 + 5000 – 100
= -5000 – 100
= -5100.
3) Le nombre d’appareils à produire pour obtenir un bénéfice maximal est donc 25 et ce bénéfice est 525 car c’est le maximum atteint par la fonction B dans le tableau de variation. Il est atteint en x = 25.
4) C(x) = x² + 50x + 100
et CM(x) = C(x)/x
Donc CM(x) = (x² + 50x + 100)/x
= x²/x + 50x/x + 100/x
= x + 50 + 100/x.
5) CM(x)
= x + 50 + 100/x
= x + 50 + u(x)/v(x)
avec
u(x) = 100,
u ‘ (x) = 0,
v(x) = x,
v ‘ (x) = 1.
Donc CM ‘ (x)
= 1 + 0 + [ u ‘ (x)×v(x) – u(x)×v ‘ (x) ]/(v(x))²
= 1 + [ 0×x – 100×1 ]/(x²)
= 1 – 100/(x²)
= x²/x² – 100/x²
= (x² − 100)/x².
6) CM ‘ (x) est un quotient composé d’un polynôme du second degré au numérateur, et d’un carré au dénominateur.
Etudions le signe du polynôme au numérateur :
Pour étudier le signe de ce polynôme du second degré, on calcule le discriminant.
Δ = b2 – 4×a×c
= 02 – 4×1×(-100)
= 400 > 0 donc deux racines.
x1 = (-b – √Δ)/(2a)
= (-0 – √400)/(2×1)
= (-0 – 20)/2
= -20/2
= -10.
x2 = (-b + √Δ)/(2a)
= (-0 + √400)/(2×1)
= (-0 + 20)/2
= 20/2
= 10.
Comme a = 1 > 0, la parabole est ouverte vers le haut (souriante car atmosphère et ambiance positives).
De plus, comme Δ > 0, elle coupe deux fois l’axe des abscisses.
Donc ce polynôme du second degré est donc positif, puis négatif, puis positif.
Voici donc le tableau de signe de CM ‘ (x) et de variation de CM :
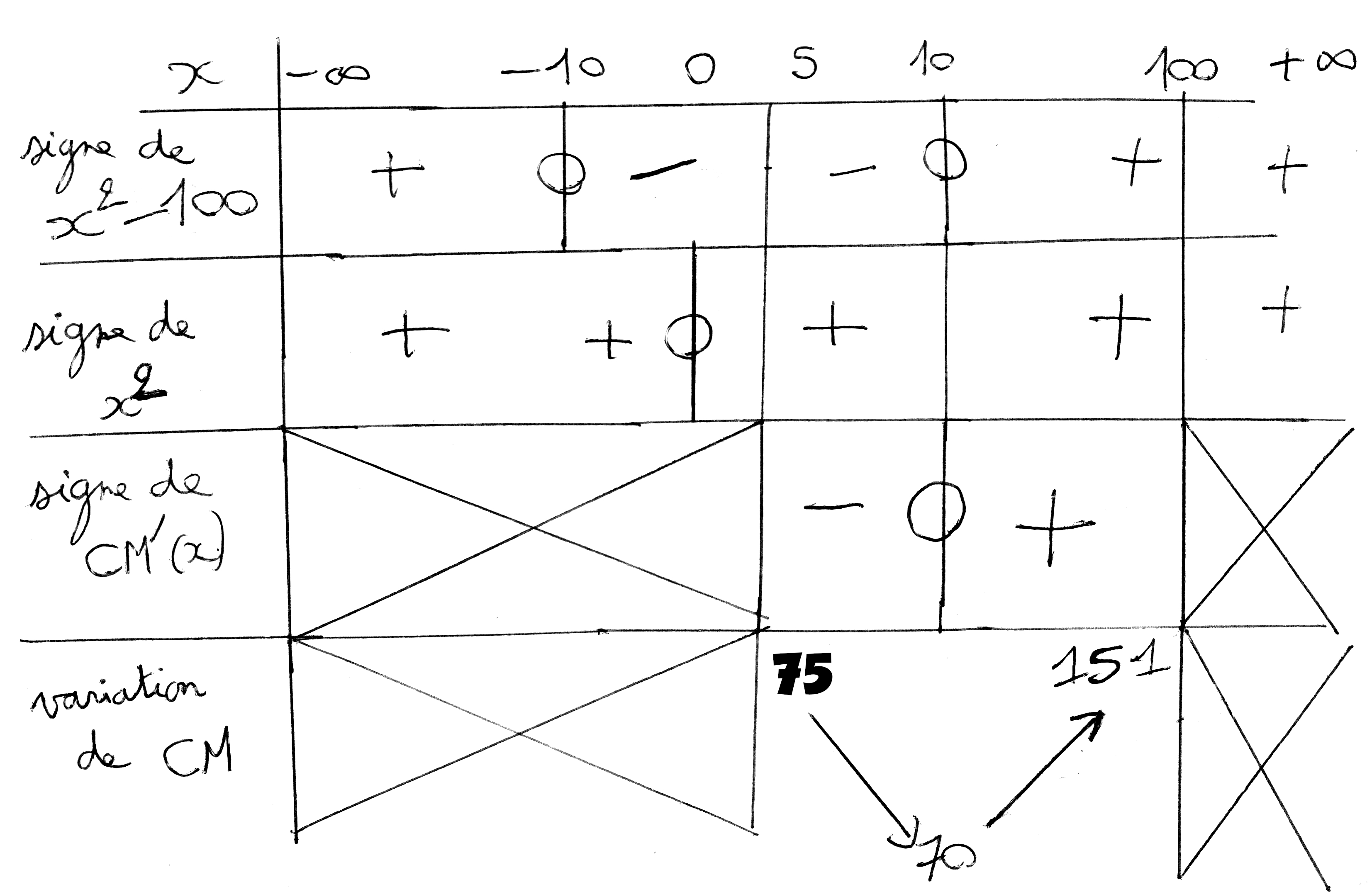
CM(5) = 5 + 50 + 100/5
= 55 + 20
= 75.
CM(10) = 10 + 50 + 100/10
= 60 + 10
= 70.
CM(100) = 100 + 50 + 100/100
= 150 + 1
= 151.
7) D’après le tableau de variation précédent, CM est minimal pour x = 10 et son minimum est 70.
8) B est maximal pour x = 25 et CM est minimal pour x = 10. Donc le bénéfice n’est pas maximal quand le coût moyen est minimal.
Bonne compréhension,
Sylvain Jeuland

