Exercice : Clic droit vers l’exercice
Tout le corrigé :
1) Je fais les calculs un par un à la calculette (ou avec le tableur). Puis je complète le tableau de la fonction
C(x) = x2 + 20x + 900.

2) Je trace la représentation graphique de la fonction C en prenant 1 cm pour 10 unités en abscisses et 1 cm pour 1000 euros en ordonnées.
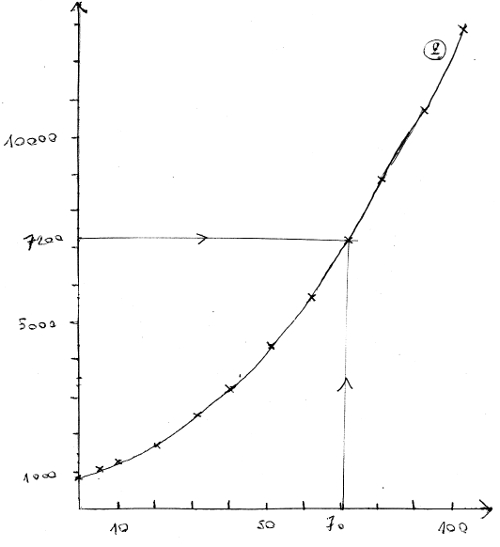
3) Pour calculer la recette R(x) obtenue avec la vente de x cartes (120 euros chacune), on fait la formule suivante :
Recette = Prix_unitaire × Quantité
Donc R(x) = 120 × x.
R(x) est une fonction affine. Pour tracer cette droite, je choisis moi-même deux valeurs x car il faut deux points pour tracer une droite.
Je choisis x = 20 et x = 80.
Pour x = 20,
y= R(10) = 120 × 20 = 2400.
Je dessine A(20 ; 2400).
Pour x = 80,
y= R(90) = 120 × 80 = 9600.
Je dessine B(80 ; 9600).
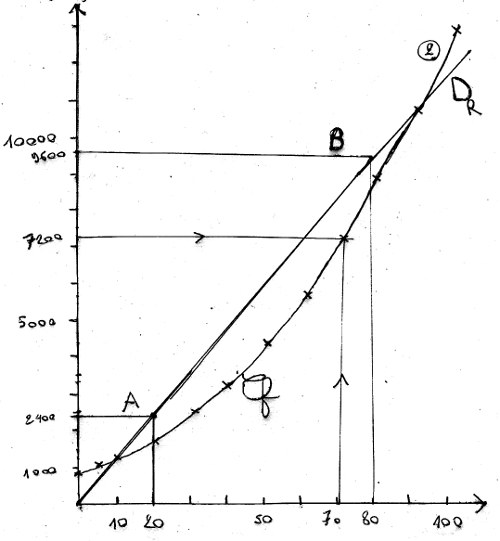
La droite représentant la recette passe toujours par l’origine. On le vérifie ici.
4) Pour exprimer le bénéfice B(x), on utilise la formule :
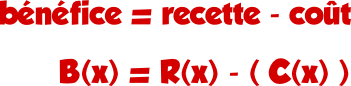
Donc B(x) = 120x – ( x2 + 20x + 900 )
= 120x – x2 – 20x – 900
Du coup, B(x) = – x2 + 100x – 900.
5) La production est rentable si et seulement si le bénéfice est positif.
Etudions le signe de B(x) en faisant un tableau de signe.
Comme nous avons une fonction du second degré, calculons le discriminant Δ :
Δ = b2 – 4ac
= 1002 – 4 × (-1) × (-900)
= 10000 – 3600
= 6400 > 0.
On obtient donc deux racines :
x1 = (-b – √Δ)/(2a)
= (-100 – √6400)/(2 × (-1))
= (-100 – 80)/(-2)
= (-180)/(-2)
= 90.
x2 = (-b + √Δ)/(2a)
= (-100 + √6400)/(2 × (-1))
= (-100 + 80)/(-2)
= (-20)/(-2)
= 10.
Comme a vaut -1, il est donc négatif. Comme Δ > 0, la parabole coupe deux fois l’axe des abscisses et on aura des changements de signe.
Comme a est positif, la parabole est souriante donc le signe du polynôme du second degré est d’abord positif, puis négatif, puis positif.
Voici le tableau de signe :
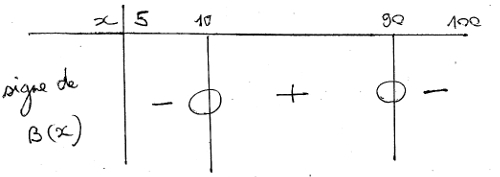
B(x) est positif sur [10 ; 90] donc la production est rentable pour x allant 10 à 90 unités.
6) Pour vérifier graphiquement quand la production est rentable, je sélectionne le ou les morceau(x) de courbe quand la recette est supérieure au coût, c’est à dire quand la droite de la recette est au dessus de la parabole du coût.
Puis je descends verticalement vers l’axe des abscisses pour sélectionner le bon intervalle de production.
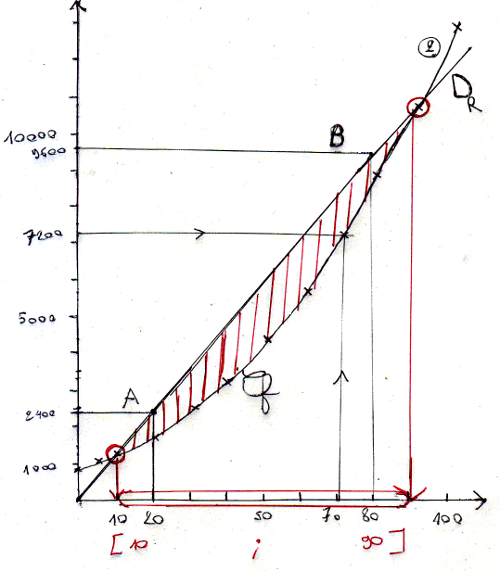
La zone entre la courbe du coût et la droite de la recette représente le bénéfice. Plus l’écart entre les deux courbes est important, plus le bénéfice est important.
Bonne compréhension,
Sylvain Jeuland

