frenchmaths.com (par Sylvain Jeuland)

Exercice : Clic droit sur l’exercice

Tout le corrigé :

Quand on calcule un éventuel nombre dérivé f ‘ (a) en x = a, on cherche à trouver ^{[ f(a+h) – f(a) ]}/_{[a+h – a]} en fonction de h.
Puis on tend ce h vers 0 pour arriver à une limite.
Si tu trouves une constante, tu obtiens que la fonction est dérivable en x = a et que ce nombre est f ‘ (a).

1)

Donc le taux de variation ^{[ f(a+h) – f(a) ]}/_{[a+h – a]} admet une limite finie en a = 2 donc le nombre f ‘ (2) existe et vaut -1.
Donc f est dérivable en 2 et f ‘ (2) = -1.

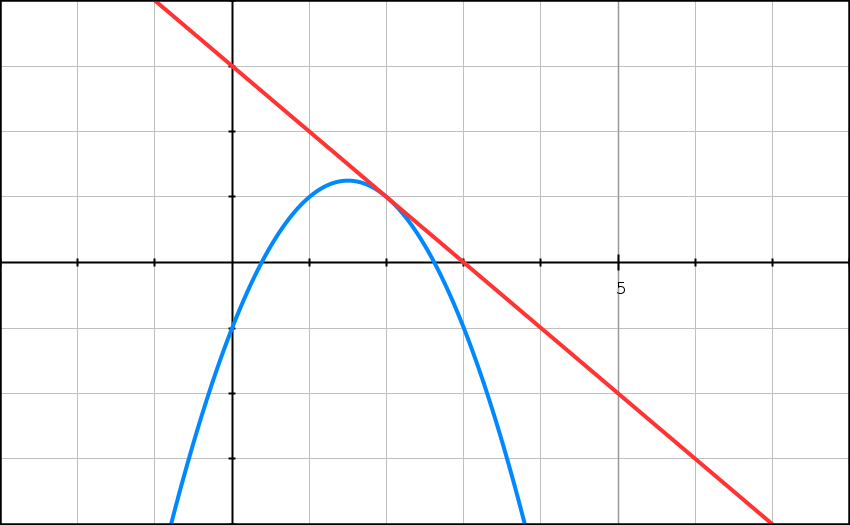
Donc le coefficient de la tangente à Cf en a = 2 est égal à -1.

2)

J’ai oublié le “h” devant la flèche “→0”.

Donc le taux de variation ^{[ f(a+h) – f(a) ]}/_{[a+h – a]} admet une limite finie en a = 4 donc le nombre f ‘ (4) existe et vaut ¹/₂.
Donc f est dérivable en 4 et f ‘ (4) = ¹/₂.

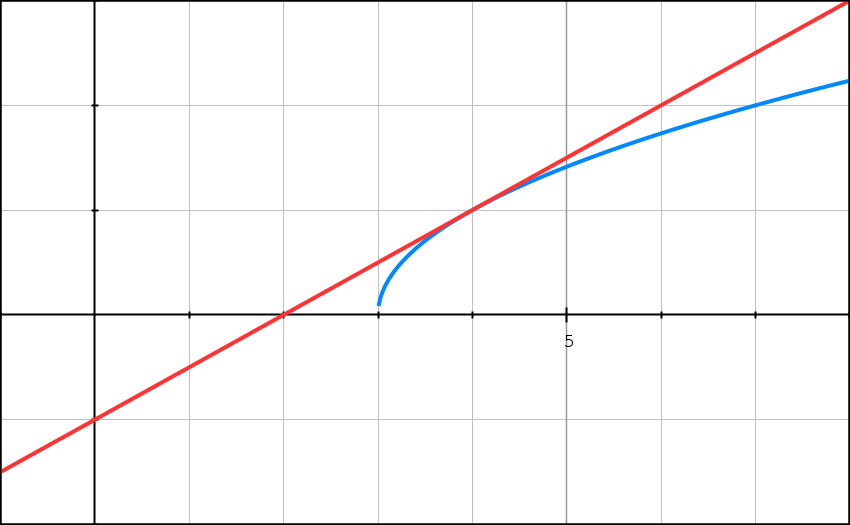
Donc le coefficient de la tangente à Cf en a = 4 est égal à ¹/₂.

3)

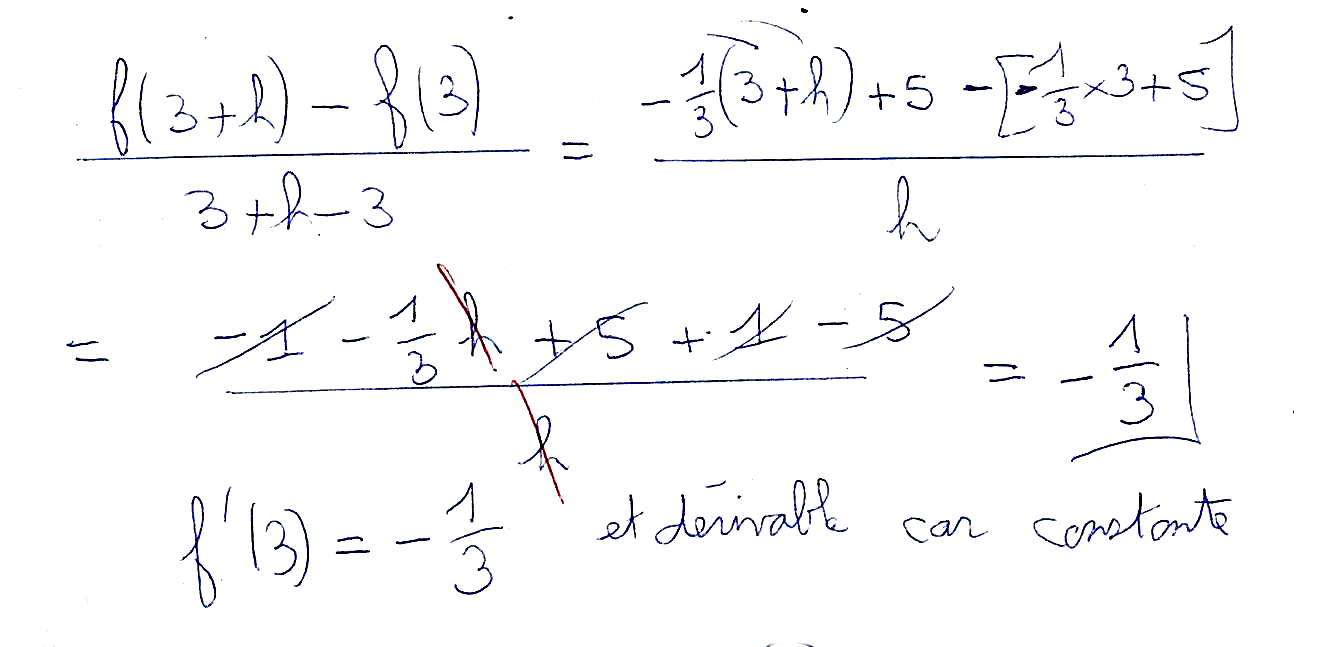
J’ai oublié le “h” devant la flèche “→0”.

Donc le taux de variation ^{[ f(a+h) – f(a) ]}/_{[a+h – a]} admet une limite finie en a = 3 donc le nombre f ‘ (3) existe et vaut –¹/₃.
Donc f est dérivable en 3 et f ‘ (3) = –¹/₃.

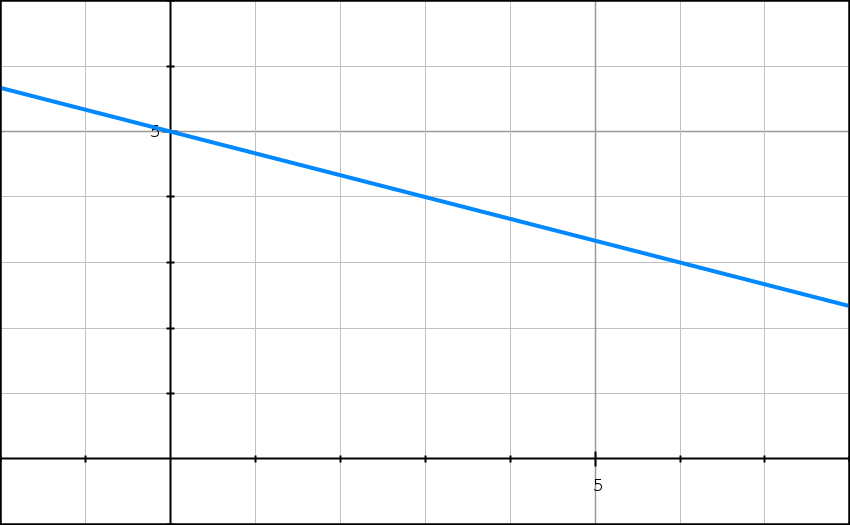
Donc le coefficient de la tangente à Cf en a = 3 est égal à –¹/₃. Comme notre fonction est affine, la tangente est la droite elle-même.

4) En a = -2, on a x + 2 = 0, donc le contenu de la valeur absolue est nul.
Or la fonction “valeur absolue” n’est pas dérivable en 0.
Donc la valeur absolue de x + 2 n’est pas dérivable en -2.
Il n’y a donc pas de nombre dérivé de |x + 2| en a = -2.

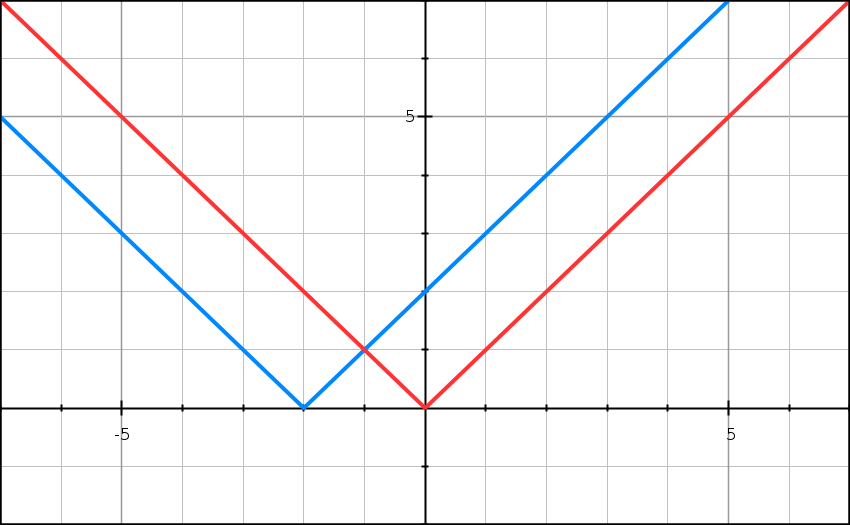
A gauche, on voit la courbe de la fonction représentant |x + 2|.
A droite, celle de |x].
En a = -2, sur la courbe de gauche, on est sur la “pointe” des deux demi-droites, il n’y a pas de tangente qui suit la courbe en a = -2.

Bonne compréhension,
laisse un commentaire en cas de problème,
Sylvain Jeuland